Question

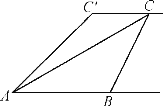
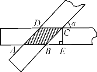
【题目】如图所示，两条宽度都为2cm的纸条交叉重叠放在一起，且它们的交角为α，则它们重叠部分(图中阴影部分)的面积为________．

Answer 1

【答案】cm2

【解析】

首先过C作CE⊥AB，CF⊥AD，垂足为E，F，证明△CEB≌△CFD，从而证明四边形ABCD是菱形，再利用三角函数算出BC的长，最后根据菱形的面积公式算出重叠部分的面积即可．

解：过C作CE⊥AB，CF⊥AD，垂足为E，F，

∴∠CEB=∠CFD=90°，

∵AD∥CB，AB∥CD，

∴四边形ABCD是平行四边形，

∵纸条宽度都为2cm，

∴CE=CF=2cm，

在△CEB和△CFD中

，

∴△CEB≌△CFD（AAS），

∴BC=CD，

∴四边形ABCD是菱形．

∴BC=AB，

在Rt△CEB中，

BC==，

∴BC=AB=，

∴重叠部分（图中阴影部分）的面积为：AB×CE=×2=cm2．

故答案为：cm2．