题目内容
问题背景:
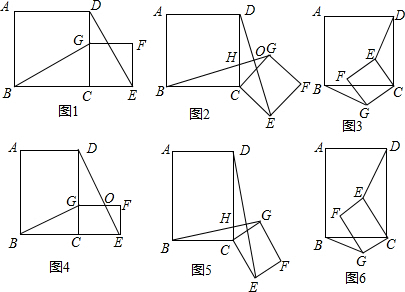
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.


(1)实践运用:
如图(b),已知,⊙O的直径C![]() D为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为__________.
D为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为__________.
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
![]() …………………4分
…………………4分
 (2)解:如图,在斜边AC上截取AB′=AB,连结BB′.
(2)解:如图,在斜边AC上截取AB′=AB,连结BB′.
∵AD平分∠BAC,
∴点B与点B′关于直线AD对称. …………6分
过点B′作B′F⊥AB,垂足为F,交AD于E,连结BE,
则线段B′F的长即为所求.(点到直线的距离最短) ………8分
在Rt△AFB/中,∵∠BAC=450, AB/=AB= 10,
![]() ,
,
∴BE+EF的最小值为![]() . ………………10分
. ………………10分

练习册系列答案
相关题目
 值,判断此时四边形EFGH的形状,并说明理由.
值,判断此时四边形EFGH的形状,并说明理由. (2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
(2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
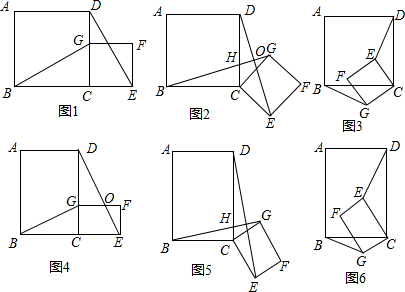 问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.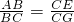 =k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.