题目内容
 二次函数y=
二次函数y=| 2 | 3 |
分析:只要求出每个菱形的边长,找出边长之间的关系就可以了,夹角为120°很特殊,菱形由两个等边三角形组成,第一个菱形在y轴上的两个顶点之间距离为其边长,同样第二个菱形边长等于第二个菱形在y轴上的两个顶点之间的距离,以此类推,只要求出各个菱形的边长就可以看出关系.
解答:解:设第一个菱形边长为b,
则第一个菱形在x轴正向与函数y=
x2交点为(
b,
)(因为其边长与x轴夹角为30°)
代入y=
x2
得b=1;
设第二个菱形边长为c,则其边长与函数交点为(
c,
c+1)代入函数表达式得c=2,
同理得第三个菱形边长为3,第n个菱形边长为n,故第2009个菱形边长为2009
∴其周长为:2009×4=8036.
故答案为:8036.
则第一个菱形在x轴正向与函数y=
| 2 |
| 3 |
| ||
| 2 |
| b |
| 2 |
代入y=
| 2 |
| 3 |
得b=1;
设第二个菱形边长为c,则其边长与函数交点为(
| ||
| 2 |
| 1 |
| 2 |
同理得第三个菱形边长为3,第n个菱形边长为n,故第2009个菱形边长为2009
∴其周长为:2009×4=8036.
故答案为:8036.
点评:此题主要考查二次函数性质和坐标表示以及菱形的性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
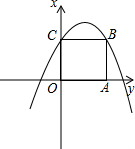 如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-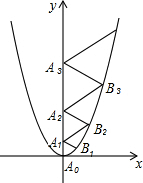 二次函数
二次函数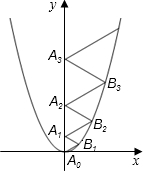 二次函数
二次函数