Question

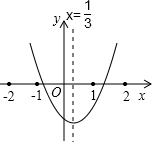
从图中的二次函数y=ax²+bx+c图象中，观察得出了下面的五条信息：
①b＞0 ②c=0  ③函数的最小值为-3  ④a-b+c＞0  ⑤当x₁＜x₂＜2时，y₁＞y₂．
（1）你认为其中正确的有哪几个？（写出编号）
（2）根据正确的条件请求出函数解析式．

Answer 1

分析：（1）根据开口方向①；根据抛物线与y轴的交点判断②；根据抛物线顶点坐标及开口方向判断③；观察当x＜0时，图象是否在x轴上方，判断④；在0＜x₁＜x₂＜2时，函数的增减性判断⑤．
（2）利用顶点式求出二次函数的解析式即可．

解答：解：（1）
根据图象可知：
①∵该函数图象的开口向上，∴a＞0，∴b＜0，（此时a，b异号）故此选项错误；
②x=0时，可y=c=0，故此选项正确；
③利用函数顶点坐标，函数的最小值为-3，故此选项正确；
④根据图象知，当x=-1时，图象是在x轴上方，∴y＞0；即a-b+c＞0，故此选项正确；
⑤当x＜2时函数为减函数，0＜x₁＜x₂＜2时，y₁＞y₂，故此选项正确．
故正确的有：②③④⑤，
（2）∵函数的顶点坐标为：（2，-3），
∴二次函数的解析式为：y=a（x-2） ²-3，
将（0，0）代入求出即可：
a=

3

4

，
∴函数解析式为：y=

3

4

（x-2） ²-3．

点评：此题考查了函数图象与抛物线系数的性质关系以及顶点式求二次函数解析式，要求数形结合，逐一判断是解题关键．