题目内容
【题目】如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°. 
(1)求证:DF∥AB;
(2)若OC=CE,BF= ![]() ,求DE的长.
,求DE的长.
【答案】
(1)证明:连接OF,
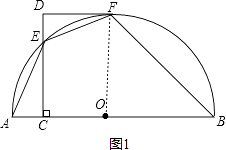
∵A、E、F、B四点共圆,
∴∠AEF+∠B=180°,
∵∠AEF=135°,
∴∠B=45°,
∴∠AOF=2∠B=90°,
∵DF切⊙O于F,
∴∠DFO=90°,
∵DC⊥AB,
∴∠DCO=90°,
即∠DCO=∠FOC=∠DFO=90°,
∴四边形DCOF是矩形,
∴DF∥AB
(2)解:过E作EM⊥BF于M,
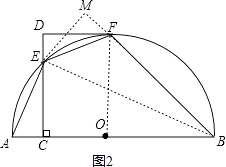
∵四边形DCOF是矩形,
∴OF=DC=OA,
∵OC=CE,
∴AC=DE,
设DE=x,则AC=x,
∵在Rt△FOB中,∠FOB=90°,OF=OB,BF=2 ![]() ,由勾股定理得:OF=OB=2,
,由勾股定理得:OF=OB=2,
则AB=4,BC=4﹣x,
∵AC=DE,OCDF=CE,
∴由勾股定理得:AE=EF,
∴∠ABE=∠FBE,
∵EC⊥AB,EM⊥BF
∴EC=EM,∠ECB=∠M=90°,
在Rt△ECA和Rt△EMF中
![]()
∴Rt△ECA≌Rt△EMF,
∴AC=MF=DE=x,
在Rt△ECB和Rt△EMB中,由勾股定理得:BC=BM,
∴BF=BM﹣MF=BC﹣MF=4﹣x﹣x=2 ![]() ,
,
解得:x=2﹣ ![]() ,
,
即DE=2﹣ ![]() .
.
【解析】(1)证明:连接OF,根据圆内接四边形的性质得到∠AEF+∠B=180°,由于∠AEF=135°,得出∠B=45°,于是得到∠AOF=2∠B=90°,由DF切⊙O于F,得到∠DFO=90°,由于DC⊥AB,得到∠DCO=90°,于是结论可得;(2)过E作EM⊥BF于M,由四边形DCOF是矩形,得到OF=DC=OA,由于OC=CE,推出AC=DE,设DE=x,则AC=x,在Rt△FOB中,∠FOB=90°,OF=OB,BF=2 ![]() ,由勾股定理得:OF=OB=2,则AB=4,BC=4﹣x,由于AC=DE,OCDF=CE,由勾股定理得:AE=EF,通过Rt△ECA≌Rt△EMF,得出AC=MF=DE=x,在Rt△ECB和Rt△EMB中,由勾股定理得:BC=BM,问题可得.
,由勾股定理得:OF=OB=2,则AB=4,BC=4﹣x,由于AC=DE,OCDF=CE,由勾股定理得:AE=EF,通过Rt△ECA≌Rt△EMF,得出AC=MF=DE=x,在Rt△ECB和Rt△EMB中,由勾股定理得:BC=BM,问题可得.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文的26个字母a、b、c,…,z依次对应1、2、3,…,26这26个自然数(见表格),当明码对应的序号x为奇数时,密码对应的序号 ![]() ;当明码对应的序号x为偶数时,密码对应的序号
;当明码对应的序号x为偶数时,密码对应的序号 ![]() .
.
字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
按上述规定,将明码“bird”译成密码是( )
A.bird
B.nove
C.sdri
D.nevo






