题目内容
如图,已知 的周长为
的周长为 ,
, ,
, .
.
(1)判断 的形状;
的形状;
(2)若 为边
为边 上的中线,
上的中线, ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,连结
,连结 .求证:
.求证: .
.

 的周长为
的周长为 ,
, ,
, .
.(1)判断
 的形状;
的形状;(2)若
 为边
为边 上的中线,
上的中线, ,
, 的平分线交
的平分线交 于点
于点 ,交
,交 于点
于点 ,连结
,连结 .求证:
.求证: .
. 
(1)△ABC是直角三角形;(2)讲明见解析.
试题分析:(1)根据△ABC的周长和两边的长,可求得AB的长,根据三边的关系判断△ABC的形状;
(2)此题要想求得面积,应该先求DE=BD=CD=
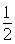 AB,可过点C作CM⊥AB交AB于M,得CM∥DE,通过角的关系证得.
AB,可过点C作CM⊥AB交AB于M,得CM∥DE,通过角的关系证得.解:(1)△ABC是直角三角形.
∵△ABC的周长是4+2
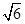 ,AB=4,AC=
,AB=4,AC=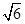 +
+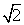 ,
,∴BC=(4+2
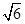 )4(
)4(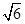 +
+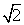 )=
)=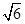 ?
?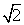 ,
,∵(
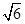 +
+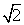 )2+(
)2+(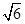 ?
?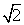 )2=42,
)2=42,∴AC2+BC2=AB2,
∴△ABC是直角三角形;
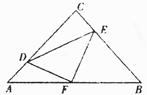
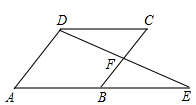
(2)过点C作CM⊥AB交AB于M,
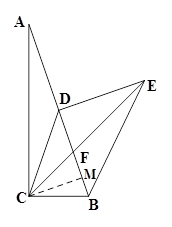
∵DE⊥AB,
∴CM∥DE,
∴∠DEF=∠MCF,
又∵AD=CD,
∴∠A=∠ACD,
∵∠BCM=∠A,
∴∠ACD=∠BCM,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠DCF=∠MCF,
∴∠DCF=∠DEF,
∴DC=DE=
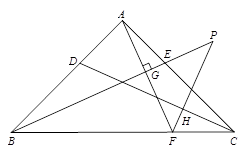
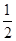 AB=2,
AB=2, 
练习册系列答案
相关题目
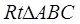 中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=4,BC=7,CD=2.
中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=4,BC=7,CD=2.