Question

【题目】规定：把一次函数y＝kx＋b的一次项系数和常数项互换得y=bx＋k，我们称y＝kx＋b和y＝bx＋k(其中k·b≠0，且|k|≠|b|))为互助一次函数，例如：y＝－2x＋3和y＝3x－2就是互助一次函数．如图1所示，一次函数y＝kx＋b和它的互助一次函数的图象1，2交于点P，1，2与x轴、y轴分别交于点A，B和点C，D．

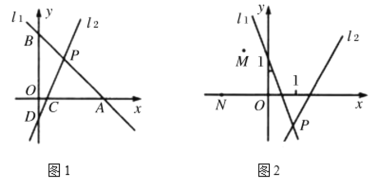
(1)如图1所示，当k＝－1，b＝5时，直接写出点P的坐标是_________．

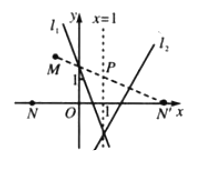
(2)如图2所示，已知点M(－1，1.5)，N(－2，0)．试探究随着k，b值的变化，MP＋NP的值是否发生变化，若不变，求出MP＋NP的值；若变化，求出使MP＋NP取最小值时点P的坐标．

Answer 1

【答案】（1）；（2）使取最小值时的点坐标为

【解析】

（1）根据互助一次函数的定义，由k＝－1，b＝5分别写出两个函数解析式，联立，解二元一次方程组，即可求出交点P的坐标；

（2）联立，解得=1，故点在直线上运动，的值随之发生变化；作N点关于的对称点，根据两点之间线段最短，可知连接对称点和M的线段就是MP＋NP的最小值，用待定系数法求出直线的函数解析式，进而求出P点坐标．

（1）联立

解得：

即P点坐标为，

故答案为：；

（2）由解得，

即，

随着值的变化，点在直线上运动，的值随之发生变化，如图所示，作点关于直线的对称点，连接交直线于点，则此时取得最小值．

设直线的函数解析式为，

分别将M(－1，1.5)和代入解析式得：

解得：

∴直线的函数解析式为：，

令，则

．

使取最小值时的点坐标为．