��Ŀ����
�Ķ����в��ϣ�
����֪�� �ļ�������������������
�ļ�������������������
 =
= ��Ҳ����˵��
��Ҳ����˵�� ��ʾ����������
��ʾ����������
 ��ʾ����������
��ʾ���������� ����
���� ��Ӧ�ĵ�֮��ľ��룻
��Ӧ�ĵ�֮��ľ��룻
��1���ⷽ��|



��2���ⲻ��ʽ|








��3���ⷽ��|












�ο��Ķ����ϣ�����������⣺
��1������|
��2���ⲻ��ʽ��|
��3���ⲻ��ʽ��|

��ϰ��ϵ�д�
�����Ŀ


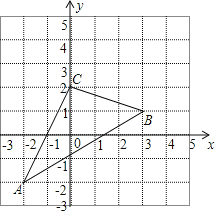

 ����ֻ���ĸ������⣬��ʹ����y�ķ���
����ֻ���ĸ������⣬��ʹ����y�ķ��� �Ľ�Ϊ�Ǹ������������������������
�Ľ�Ϊ�Ǹ������������������������







 �Ķ���Ϊ�� ��
�Ķ���Ϊ�� ��
 +1��y=
+1��y= ��ֵ��
��ֵ��
 ����
����