题目内容
如图,在△ABC中,∠BAC=90°,AB=9,AC=12,AD⊥BC,垂足为D.

(1)求BC的长;(2)求BD的长.
(1)15(2)
【解析】
试题分析:(1)由已知在△ABC中,∠BAC=90°,所以得到△ABC为直角三角形且AB、AC为两直角边,因此根据勾股定理可求出BC的长.(2)AD⊥BC,垂足为D,所以得到直角三角形DBA,∠BDA和∠BAC都为直角,∠B为公共角,得到△ABC与△DBA相似,根据相似三角形的性质求得BDA.
【解析】
(1)在△ABC中,∵∠BAC=90°,
∴BC2=AB2+AC2(勾股定理),
=92+122,
=81+144,
=225.
∴BC=15.
(2)AD⊥BC,垂足为D,
∴△DBA为直角三角形,
在△ABC与△DBA中,
∠BDA=∠BAC=90°,∠B=∠B(公共角),
∴△ABC∽△DBA,
∴ =
= ,
,
∴BD=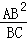 =
= =
= .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
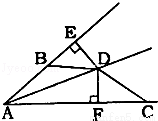

 ,点D为AC的中点,点E在边BC上,且ED⊥BD,则△CDE的面积是 .
,点D为AC的中点,点E在边BC上,且ED⊥BD,则△CDE的面积是 .

