Question

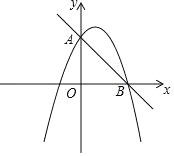
【题目】如图，己知抛物线与轴相交于点，其对称轴与抛物线相交于点，与轴相交于点．

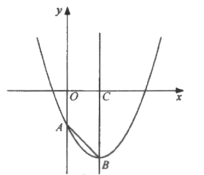
（1）求的长；

（2）平移该抛物线得到一条新抛物线，设新抛物线的顶点为．若新抛物线经过原点，且，求新抛物线对应的函数表达式．

Answer 1

【答案】（1）；（2）或

【解析】

（1）先利用函数关系式求出点A、B的坐标，再利用两点间的距离公式即可求得AB的长；

（2）根据A、B两点坐标结合三角函数可求得∠POA＝∠ABC＝45°，进而可判断点P在在一、三象限或二、四象限的角平分线上，分情况讨论，设点P坐标为（a，a）或（-a，a），利用顶点式表示出新抛物线的函数表达式，再将原点O的坐标代入计算即可．

解：（1）当x＝0时，y＝-1，

∴点A坐标为（0，-1），

∵

∴

∴点B坐标为（1，-2），

∴；

（2）∵点A坐标为（0，-1），点B坐标为（1，-2），

∴tan∠ABC＝，

∴∠ABC＝45°，

∵∠POA＝∠ABC，

∴∠POA＝45°，

∴点P在一、三象限或二、四象限的角平分线上，

当点P在一、三象限的角平分线上时，

设点P坐标为（a，a）

则设此时新抛物线的解析式为

∵新抛物线经过原点，

∴将（0，0）代入，得

解得（舍去）

∴，

即，

当点P在二、四象限的角平分线上时，

设点P坐标为（-a，a）

则设此时新抛物线的解析式为

∵新抛物线经过原点，

∴将（0，0）代入，得

解得（舍去）

∴，

即，

综上所述，新抛物线对应的函数表达式为或．