Question

【题目】在平面直角坐标系中，有三点，且满足：

（1）求A、B、C三点坐标；

（2）已知，在y轴上有一点 ，在坐标轴上是否存在一点P，使△ABP和△ABC的面积相等？若存在，求出P点坐标．若不存在，请说明理由．（C点除外）

Answer 1

【答案】（1） （2）P（0，5）或P（0，-2）或P（-10，0）

【解析】

（1）根据算术平方根的非负性、绝对值的非负性、平方的非负性结合已知条件得出且且，解出a、b、c的值即可；

（2）分①当点P在y轴上时，②当点P在x轴上时两种情况讨论，先求出△ABC的面积，再设出点P的坐标，列出△ABP面积的表达式，进而利用△ABP和△ABC的面积相等得到方程，解方程即可.

解：（1）∵，且≥0，≥0，≥0，

∴且且，

解得：a=-3，b=3，c=4，

∴A、B、C三点坐标分别为：，，.

（2）在坐标轴上存在点P，使△ABP和△ABC的面积相等.理由如下：

如下图1，过点B作BE⊥AC，由第（1）问得：AC=7，BE=3，

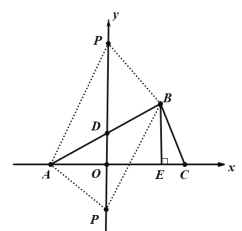
图1

S△ABC=AC·BE=.

①当点P在y轴上时，设点P的坐标为（0，y），

S△ABP=PD·AO+PD·OE=PD·(AO+OE) =PD·AE= ·|y-|×6，

∵S△ABP= S△ABC

∴·|y-|×6=，

解得：y=5或y=-2，

∴点P的坐标为（0，5）或（0，-2）；

②当点P在x轴上时，设点P的坐标为（x，0），如下图2：

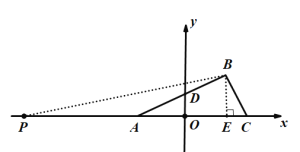
图2

S△ABP=AP·BE=·|-3-x|×3，

∵S△ABP= S△ABC

∴·|-3-x|×3=，

解得：x=-10或x=4（舍去），

∴点P的坐标为（-10，0）.

综上，在坐标轴上存在点P，使△ABP和△ABC的面积相等，点P的坐标为（0，5）或（0，-2）或（-10，0）.