题目内容
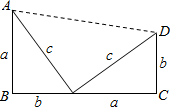利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理，此证明方法就是美国第二十任总统伽菲尔德最先完成的，人们为了纪念他，把这一证法称为“总统”证法．这个定理称为________，该定理的结论其数学表达式是________．
勾股定理 a2+b2=c2
分析：利用两个直角边分别为a、b的直角三角形构造直角梯形，然后将直角梯形的面积化为三个直角三角形的面积的和解答．
解答：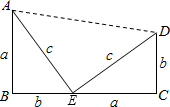
解：如图，
∵∠AEB=∠EDC，
∴∠AEB+∠DEC=90°，
∴S△AED=
c2，
∵S△ABE=S△DEC=ab，
又∵S梯形ABCD=（a+b）（a+b）=（a2+2ab+b2）．
∴S△AED+S△ABE+S△DEC=S梯形ABCD，
c2+ab+ab=（a2+2ab+b2 ），
整理得，a2+b2=c2．
点评：本题考查了勾股定理的证明，这是总统证法，将梯形的面积，转化为几个直角三角形的和是解题的关键．
分析：利用两个直角边分别为a、b的直角三角形构造直角梯形，然后将直角梯形的面积化为三个直角三角形的面积的和解答．
解答：
解：如图，∵∠AEB=∠EDC，
∴∠AEB+∠DEC=90°，
∴S△AED=
c2，∵S△ABE=S△DEC=
ab，又∵S梯形ABCD=
（a+b）（a+b）=（a2+2ab+b2）．∴S△AED+S△ABE+S△DEC=S梯形ABCD，
c2+ab+ab=（a2+2ab+b2 ），整理得，a2+b2=c2．
点评：本题考查了勾股定理的证明，这是总统证法，将梯形的面积，转化为几个直角三角形的和是解题的关键．
练习册系列答案
相关题目
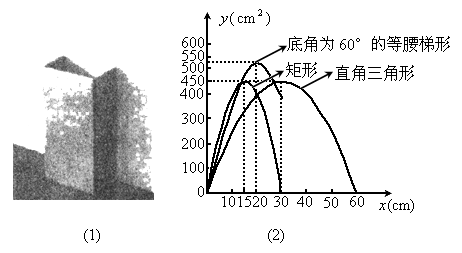
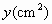与x(cm)(见表中横截面图形所示)的函数关系式而绘制出的图象．请你根据有关信息，在表中空白处填上适当的数、式，并完成y取最大值时的设计示意图；
(2)在研究性学习小组展示研究成果时，小华同学指出：图(2)中“底角为60°的等腰梯形”的图象与其他两个图象比较，还缺少一部分，应该补画．你认为他的说法正确吗?请简要说明理由．