题目内容
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线。如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则经过点D的“蛋圆”的切线的解析式为__________________。
y=-2x-3
解析试题分析:解:求切线解析式需要先求出二次函数解析式,因为切线过点D,所以切线解析式与二次函数解析式组成方程组,因只有一个交点,所以判别式为零。∵M(1,0)半径=2,∴A(-1,0),B(3,0),又D(0,-3),设二次函数的解析式为y=a(x-x1)(x-x2),将点A,B,C代入得;-3a=-3,∴a=1,∴y=(x+1)(x-3)=x2-2x-3.∵切线与蛋圆只有一个交点,且经过点D,设切线解析式为y=kx+b,∵过点D,∴b=-3,x2-2x-3="kx-3" ,即-(2+k)2=0,∵只有一个交点,∴判别式△=0,解得k=-2,∴y=-2x-3.
考点:二次函数的定义及性质,一次函数的定义,一元二次方程的判别式求根的方法。
点评:熟知以上几个性质,定义及方法。在解题时找到两个函数的共同点,及都过一点,要注意的是,一元二次方程有一解时,判别式△=0.从而求之,本题属于偏难题型,属于中档题。

练习册系列答案
相关题目
 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为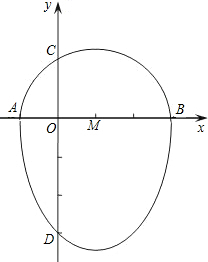 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.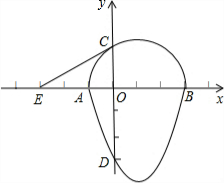 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是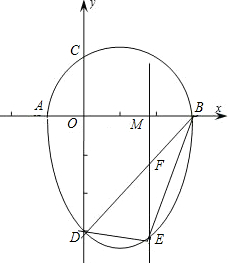 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标. 仔细阅读并完成下题:
仔细阅读并完成下题: