题目内容
13.已知一次函数y=(1-3k)x-(2-k).(1)k为何值时,y随x的增大而减小?
(2)k为何值时,该直线与y轴的交点在x轴下方?
(3)k为何值时,该直线不经过第一象限?
分析 (1)要使y随x的增大而减小,只需一次项的系数小于0即可;
(2)要使直线与y轴的交点在x轴下方,只需直线与y轴的交点的纵坐标小于0即可;
(3)直线不经过第一象限,有两种可能(①经过二、三、四象限,②只经过二、四象限),只需一次项的系数小于0,且直线与y轴的交点的纵坐标小于等于0即可.
解答 解:(1)当1-3k<0即k>$\frac{1}{3}$时,y随x的增大而减小;
(2)当-(2-k)<0且1-3k≠0即k<2且k≠≠$\frac{1}{3}$时,该直线与y轴的交点在x轴下方;
(3)当$\left\{\begin{array}{l}{1-3k<0}\\{-(2-k)≤0}\end{array}\right.$即$\frac{1}{3}$<k≤2时,该直线不经过第一象限.
点评 本题主要考查了一次函数的图象与系数的关系,需要注意的是“直线不经过第一象限”与“直线经过二、三、四象限”不同,不能混淆.

练习册系列答案
相关题目
18.下列一元一次方程的解是x=3的是( )
| A. | 3x+9=0 | B. | x=10-4x | C. | 2x+1=7 | D. | 2x-7=12 |
5.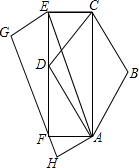 如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
 如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )| A. | S1>S2>S3 | B. | S1<S2<S3 | C. | S1=S2=S3 | D. | S1>S2>S3 |