题目内容
在平面直角坐标系xOy中，点P在由直线y=-x+3，直线y=4和直线x=1所围成的区域内或其边界上，点Q在x轴上．若点R的坐标为R（2，2），则QP+QR的最小值为 ．
考点：一次函数综合题
专题：
分析：本题需先根据题意画出图形，再确定出使QP+QR最小时点Q所在的位置，然后求出QP+QR的值即可．
解答：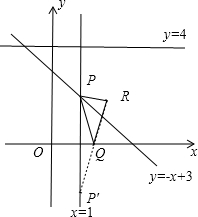
解：当点P在直线y=-x+3和x=1的交点上时，
作P关于x轴的对称点P′，连接P′R，交x轴于Q，此时PQ+QR最小，
连接PR，
∵PR=1，PP′=4，
∴P′R=
=
，
∴QP+QR的最小值为
．
故答案为：
．
解：当点P在直线y=-x+3和x=1的交点上时，作P关于x轴的对称点P′，连接P′R，交x轴于Q，此时PQ+QR最小，
连接PR，
∵PR=1，PP′=4，
∴P′R=
| 12+42 |
| 17 |
∴QP+QR的最小值为
| 17 |
故答案为：
| 17 |
点评：本题主要考查了一次函数综合问题，在解题时要能画出图形确定出Q点的位置是本题的关键，是一道常考题．
练习册系列答案
相关题目
一个数的立方根等于这个数的算术平方根，则此数是（ ）
| A、0或1 | B、0，-1和1 |
| C、0或-1 | D、-1和1 |
若代数式3x2+5x的值为5，则代数式10x-9+6x2的值是（ ）
| A、-1 | B、1 | C、5 | D、10 |
如图所示，在△ABC中，AB=AC，M，N分别是AB，AC的中点，D，E为BC上的点，连接DN，EM．若AB=10cm，BC=16cm，DE=4cm，则图中阴影部分的面积为（ ）| A、2 | B、3 | C、4 | D、6 |
如图，AB为⊙O的直径，D是⊙O 上一点，过D点作直线EF，BH⊥EF交⊙O于点C，垂足为H，且BD平分∠ABH．
连接对角线互相垂直的四边形各边中点得到的四边形是（ ）
| A、一般四边形 | B、平行四边形 |
| C、矩形 | D、菱形 |
如图，在△ABC中，D，E分别是AB和AC的中点，F是BC的延长线上一点，DF平分CE于G，已知CF=1cm，求BC的长．