题目内容
【题目】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点A（﹣3，4）、B（﹣3，0）、C（﹣1，0）．以D为顶点的抛物线y=ax2+bx+c过点B．动点P从点D出发，沿DC边向点C运动，同时动点Q从点B出发，沿BA边向点A运动，点P、Q运动的速度均为每秒1个单位，运动的时间为t秒．过点P作PE⊥CD交BD于点E，过点E作EF⊥AD于点F，交抛物线于点G．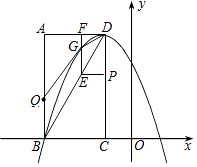
（1）求抛物线的解析式；
（2）当t为何值时，四边形BDGQ的面积最大？最大值为多少？
（3）动点P、Q运动过程中，在矩形ABCD内（包括其边界）是否存在点H，使以B，Q，E，H为顶点的四边形是菱形，若存在，请直接写出此时菱形的周长；若不存在，请说明理由．
【答案】
（1）
解：由题意得，顶点D点的坐标为（﹣1，4）．
设抛物线的解析式为y=a （x+1）2+4（a≠0），
∵抛物线经过点B（﹣3，0），代入y=a （x+1）2+4
可求得a=﹣1
∴抛物线的解析式为y=﹣（x+1）2+4，即y=﹣x2﹣2x+3
（2）
解：由题意知，DP=BQ=t，
∵PE∥BC，
∴△DPE∽△DBC．
∴ 
= 
=2，
∴PE= 
DP= t．
∴点E的横坐标为﹣1﹣ t，AF=2﹣ t．
将x=﹣1﹣ t代入y=﹣（x+1）2+4，得y=﹣ 
t2+4．
∴点G的纵坐标为﹣ t2+4，
∴GE=﹣ t2+4﹣（4﹣t）=﹣ t2+t．
如图1所示：连接BG．
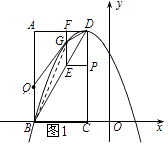
S四边形BDGQ=S△BQG+S△BEG+S△DEG，即S四边形BDGQ= BQAF+ EG（AF+DF）
= t（2﹣ t）﹣ t2+t．
=﹣ t2+2t=﹣ （t﹣2）2+2．
∴当t=2时，四边形BDGQ的面积最大，最大值为2
（3）
解：存在．
∵CD=4，BC=2，
∴tan∠BDC= ，BD=2 
．
∴cos∠BDC= 
．
∵BQ=DP=t，
∴DE= 
t．
如图2所示：当BE和BQ为菱形的邻边时，BE=QB．
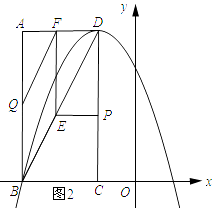
∵BE=BD﹣DE，
∴BQ=BD﹣DE，即t=2 ﹣ 
t，解得t=20﹣8 ．
∴菱形BQEH的周长=80﹣32 ．
如图3所示：当BE为菱形的对角时，则BQ=QE，过点Q作QM⊥BE，则BM=EM．
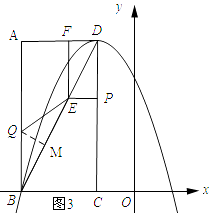
∵MB=cos∠QBMBQ，
∴MB= t．
∴BE= 
t．
∵BE+DE=BD，
∴ t+ t=2 ，解得：t= 
．
∴菱形BQEH的周长为 
．
综上所述，菱形BQEH的周长为 或80﹣32
【解析】（1）先求得点D的坐标，设抛物线的解析式为y=a （x+1）2+4（a≠0），将点B的坐标代入可求得a的值，故此可得到抛物线的解析式；（2）由题意知，DP=BQ=t，然后证明△DPE∽△DBC，可得到PE= t，然后可得到点E的横坐标（用含t的式子表示），接下来可求得点G的坐标，然后依据S四边形BDGQ=S△BQG+S△BEG+S△DEG ， 列出四边形的面积与t的函数关系式，然后依据利用配方法求解即可；（3）首先用含t的式子表示出DE的长，当BE和BQ为菱形的邻边时，由BE=QB可列出关于t的方程，从而可求得t的值，然后可求得菱形的周长；当BE为菱形的对角时，则BQ=QE，过点Q作QM⊥BE，则BM=EM．然后用含t的式子表示出BE的长，最后利用BE+ED=BD列方程求解即可．
