题目内容
如果对于任意的x,代数式x2+x+m的值都是正数,那么m的取值范围是 .
考点:配方法的应用,非负数的性质:偶次方
专题:计算题
分析:原式配方变形后,利用非负数的性质列出不等式,求出不等式的解集即可确定出m的范围.
解答:解:由题意得:x2+x+m=x2+x+
+m-
=(x+
)2+m-
>0,
∴m-
>0,
解得:m>
,
故答案为:m>
.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴m-
| 1 |
| 4 |
解得:m>
| 1 |
| 4 |
故答案为:m>
| 1 |
| 4 |
点评:此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、两点之间,线段最短 |
| B、射线OA与射线AO是同一条射线 |
| C、若线段AB=BC,则B是线段AC的中点 |
| D、连结两点的线段叫做这两点间的距离 |
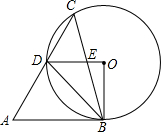 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:①DO∥AB;②CD=AD;③△BDE∽△BCD;④
| BE |
| DE |
| 2 |
正确的有( )
| A、①② | B、①③ |
| C、①②③④ | D、①③④ |
下列说法正确的是( )
| A、绝对值最小的数是0 |
| B、平方等于它本身的数是1 |
| C、1是最小的有理数 |
| D、任何有理数都有倒数 |