题目内容
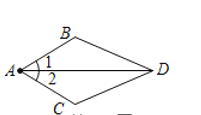
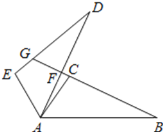
【题目】如图，已知AB＝AD，BC＝DE，且∠CAD＝10°，∠B＝∠D＝25°，∠EAB＝120°，则∠EGF的度数为___．
【答案】115°
【解析】
先得出△ABC≌△ADE,可以得出∠CAB=∠EAD=55°则∠AFG=90°,再根据三角形内角和得出∠AED,就可以算出∠EGF.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
∴∠CAB=∠EAD=55°.
根据外角定理:∠AFG=∠DAB+∠B=∠CAD+∠CAB+∠B=10°+55°+25°=90°.
在△BED中,∠E=180°－∠EAD－∠D=180°－55°－25°=100°.
在四边形AFGE中,∠EGF=360°－∠E－∠AFG－∠EAD=115°.
故答案为:115°.
练习册系列答案
相关题目
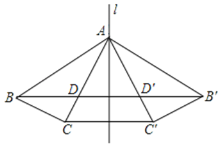
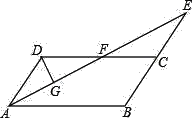
【题目】如图，在平行四边形ABCD中，∠BAD的平分线与BC的延长线交于点E，与DC交于点F．
（1）求证：CD=BE；
（2）若AB=4，点F为DC的中点，DG⊥AE，垂足为G，且DG=1，求AE的长．
【题目】某批彩色弹力球的质量检验结果如下表：
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
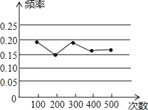
（1）请在图中完成这批彩色弹力球“优等品”频率的折线统计图
（2）这批彩色弹力球“优等品”概率的估计值大约是多少？（精确到0.01）
（3）从这批彩色弹力球中选择5个黄球、13个黑球、22个红球，它们除了颜色外都相同，将它们放入一个不透明的袋子中，求从袋子中摸出一个球是黄球的概率．
（4）现从第（3）问所说的袋子中取出若干个黑球，并放入相同数量的黄球，搅拌均匀，使从袋子中摸出一个黄球的概率为
，求取出了多少个黑球？
