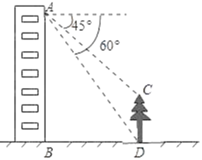
��Ŀ����
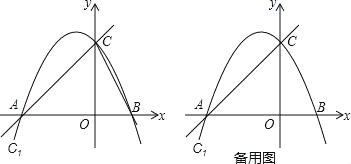
����Ŀ����֪����ͼ���ڵ���![]() �У�
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ������
������![]() ���ٶ���
���ٶ���![]() �����˶�������
�����˶�������![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ������ͬ�����ٶ���
������ͬ�����ٶ���![]() ���ӳ��߷��������˶�������
���ӳ��߷��������˶�������![]() �����
�����![]() ʱ����
ʱ����![]() ��
��![]() ͬʱֹͣ�˶������˶�ʱ��Ϊ
ͬʱֹͣ�˶������˶�ʱ��Ϊ![]()
![]() .����
.����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() Ϊ����ƽ���ı���
Ϊ����ƽ���ı���![]() .
.
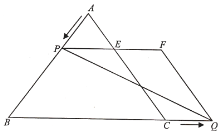
��1����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��2�����ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��4���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��ƽ�����ϣ������ڣ����
��ƽ�����ϣ������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
���𰸡�(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ��
��![]() �����ɼ�����;(4)
�����ɼ�����;(4) ![]() �����ɼ�����.
�����ɼ�����.
��������
��1������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊֱ�������Σ���������ֻ��
Ϊֱ�������Σ���������ֻ��![]() ����
����![]() ��Ȼ���ɶ�Ӧ�߳ɱ�������������⣻
��Ȼ���ɶ�Ӧ�߳ɱ�������������⣻
��2������![]() ��
��![]() �ڵ�
�ڵ�![]() ����֤
����֤![]() ��Ȼ���ɶ�Ӧ�߳ɱ����������̣����PM�ı���ʽ����֤
��Ȼ���ɶ�Ӧ�߳ɱ����������̣����PM�ı���ʽ����֤![]() �Ӷ����PE�ı���ʽ��Ȼ�������������ʽ���ɵõ�������ϵʽ��
�Ӷ����PE�ı���ʽ��Ȼ�������������ʽ���ɵõ�������ϵʽ��
��3�������ABC�����������������з�����⣻
��4����������![]() ��
��![]() ��ƽ�����ϣ��ɽ�ƽ����ƽ����
��ƽ�����ϣ��ɽ�ƽ����ƽ����![]() ������������⼴��.
������������⼴��.
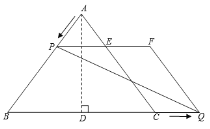
�⣺��1������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
![]()
![]()
![]()
��![]() Ϊֱ�������Σ���������ֻ��
Ϊֱ�������Σ���������ֻ��![]()
![]()
![]()
![]()
��![]()
��ã�![]()
�𣺵�![]() =
=![]() ʱ��
ʱ��![]() Ϊֱ��������.
Ϊֱ��������.
��2����![]() ��
�У�![]()
����![]() ��
��![]() �ڵ�
�ڵ�![]()
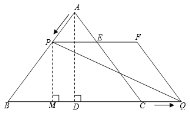
![]()
![]()
![]()
![]()
![]()
![]()
��![]()
![]()
![]()
![]() ��
��![]()
![]()
![]()
��![]()
![]()
![]() �ı���
�ı���![]() ��ƽ���ı���
��ƽ���ı���
![]()
![]()
![]()
![]()
��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��![]() .
.
��3����![]() ����
����![]()
![]()
![]()
���![]() ��
��![]()
��![]() ��ֵΪ
��ֵΪ![]() ��
��![]() ʱ��
ʱ��![]()
��4������![]()
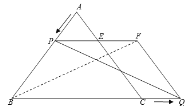
����![]() ��
��![]() ��ƽ������
��ƽ������
![]() ƽ��
ƽ��![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]()
![]()
����![]()
![]()
�𣺵�![]() ʱ����
ʱ����![]() ��
��![]() ��ƽ������.
��ƽ������.