题目内容
如图在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各个内角的度数.

答案:
解析:
提示:
解析:
|
因为 AB=AC,BC=BD=AD,所以 ∠ ABC=∠ACB=∠CDB∠ A=∠ABD又∠ CDB=∠A+∠ABD,设∠ A=x,则有x+4x=180°解之得 x=36°,所以∠ ABC=∠ACB=72°. |
提示:
|
观察图形中的关于角的数量关系 (三角形的内角、外角、等腰三角形的底角)可以发现:∠ABC=∠ACB=∠CDB=∠A+∠ABD;∠A=∠ABD;∠A+2∠C=180°,若设∠A=x,则有x+4x=180°,得到x=36°,进一步得到两个底角度数. |

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目

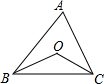 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是