题目内容
 如图,正六边形ABCDEF的边长为2
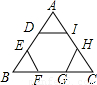
如图,正六边形ABCDEF的边长为2 cm,点P为六边形内任一点.则点P到各边距离之和为________cm.
cm,点P为六边形内任一点.则点P到各边距离之和为________cm.
18
分析:过P作AB的垂线,交AB、DE分别为H、K,连接BD,由正六边形的性质可知AB∥DE,AF∥CD,BC∥EF,故HK⊥DE,过C作CG⊥BD,由等腰三角形的性质及正六边形的内角和定理可知,DB⊥AB⊥DE,再由锐角三角函数的定义可求出BG的长,进而可求出BD的长,由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长,故可得出结论.
解答:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2 ×
× =6,
=6,
∴点P到各边距离之和为3BD=3×6=18.
故答案为:18.
点评:本题考查的是正多边形和圆及锐角三角函数的定义、特殊角的三角函数值,根据题意画出图形,利用数形结合求解时是解答此题的关键.
分析:过P作AB的垂线,交AB、DE分别为H、K,连接BD,由正六边形的性质可知AB∥DE,AF∥CD,BC∥EF,故HK⊥DE,过C作CG⊥BD,由等腰三角形的性质及正六边形的内角和定理可知,DB⊥AB⊥DE,再由锐角三角函数的定义可求出BG的长,进而可求出BD的长,由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长,故可得出结论.
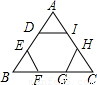
解答:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,

∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2
 ×
× =6,
=6,∴点P到各边距离之和为3BD=3×6=18.
故答案为:18.
点评:本题考查的是正多边形和圆及锐角三角函数的定义、特殊角的三角函数值,根据题意画出图形,利用数形结合求解时是解答此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
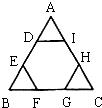 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是