题目内容
已知:如图,正方形ABCD,对角线AC、BD相交于O,Q为线段DB上的一点,∠MQN=90°,点M、N分别在直线BC、DC上,(1)如图1,当Q为线段OD的中点时,求证:DN+
 BM=
BM= BC;
BC;(2)如图2,当Q为线段OB的中点,点N在CD的延长线上时,则线段DN、BM、BC的数量关系为______;
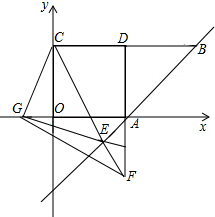
(3)在(2)的条件下,连接MN,交AD、BD于点E、F,若MB:MC=3:1,NQ=
 ,求EF的长.
,求EF的长.
【答案】分析:(1)如图1,过Q点作QP⊥BD交DC于P,然后根据正方形的性质证明△QPN∽△QBM,就可以得出结论;
(2)如图2,过Q点作QH⊥BD交BC于H,通过证明△QHM∽△QDN,由相似三角形的性质就可以得出结论;
(3)由条件设CM=x,MB=3x,就用CB=4x,得出BH=2x,由(2)相似的性质可以求出MQ的值,再根据勾股定理就可以求出MN的值,可以表示出ND,由△NDE∽△NCM就可以求出NE,也可以表示出DE,最后由△DEF∽△BMF而求出结论.
解答: 解:(1)如图1,过Q点作QP⊥BD交DC于P,
解:(1)如图1,过Q点作QP⊥BD交DC于P,
∴∠PQB=90°.
∵∠MQN=90°,
∴∠NQP=∠MQB,
∵四边形ABCD是正方形,
∴CD=CB,∠BDC=∠DBC=45°.DO=BO
∴∠DPQ=45°,DQ=PQ.
∴∠DPQ=∠DBC,
∴△QPN∽△QBM,
∴ .
.
∵Q是OD的中点,且PQ⊥BD,
∴DO=2DQ,DP= DC
DC
∴BQ=3DQ.DN+NP= BC,
BC,
∴BQ=3PQ,
∴ ,
,
∴NP= BM.
BM.
∴DN+ BM=
BM= BC.
BC.
(2)如图2,过Q点作QH⊥BD交BC于H,
∴∠BQH=∠DQH=90°,
∴∠BHQ=45°.
∵∠COB=45°,
∴QH∥OC.
∵Q是OB的中点,
∴BH=CH= BC.
BC.
∵∠NQM=90°,
∴∠NQD=∠MQH,
∵∠QND+∠NQD=45°,∠MQH+∠QMH=45°
∴∠QND=∠QMH,
∴△QHM∽△QDN,
∴ ,
,
∴HM= ND,
ND,
∵BM-HM=HB,
∴ .
.
故答案为:
(3)∵MB:MC=3:1,设CM=x,
∴MB=3x,
∴CB=CD=4x,
∴PB=2x,
∴PM=x.
∵HM= ND,
ND,
∴ND=3x,
∴CN=7x
∵四边形ABCD是正方形,
∴ED∥BC,
∴△NDE∽△NCM,△DEF∽△BMF,
∴ ,
, ,
,
∴ ,
,
∴DE= ,
,
∴
∵NQ= ,
,
∴QM=3 ,
,
在Rt△MNQ中,由勾股定理得:
MN= =15
=15 .
.
∴ ,
,
∴NE=
∴EM=
设EF=a,则FM=7a,
∴a+7a=
∴a=
点评:本题是一道相似的综合试题,考查了正方形的性质的运用,相似三角形的判定于性质的运用,勾股定理的运用及平行线等分线段定理的运用,在解答时利用三角形相似的性质求出线段的比是解答本题的关键.
(2)如图2,过Q点作QH⊥BD交BC于H,通过证明△QHM∽△QDN,由相似三角形的性质就可以得出结论;
(3)由条件设CM=x,MB=3x,就用CB=4x,得出BH=2x,由(2)相似的性质可以求出MQ的值,再根据勾股定理就可以求出MN的值,可以表示出ND,由△NDE∽△NCM就可以求出NE,也可以表示出DE,最后由△DEF∽△BMF而求出结论.
解答:
 解:(1)如图1,过Q点作QP⊥BD交DC于P,
解:(1)如图1,过Q点作QP⊥BD交DC于P,∴∠PQB=90°.
∵∠MQN=90°,
∴∠NQP=∠MQB,
∵四边形ABCD是正方形,
∴CD=CB,∠BDC=∠DBC=45°.DO=BO
∴∠DPQ=45°,DQ=PQ.
∴∠DPQ=∠DBC,
∴△QPN∽△QBM,
∴
 .
.∵Q是OD的中点,且PQ⊥BD,
∴DO=2DQ,DP=
 DC
DC∴BQ=3DQ.DN+NP=
 BC,
BC,∴BQ=3PQ,
∴
 ,
,∴NP=
 BM.
BM.∴DN+
 BM=
BM= BC.
BC.(2)如图2,过Q点作QH⊥BD交BC于H,
∴∠BQH=∠DQH=90°,
∴∠BHQ=45°.
∵∠COB=45°,
∴QH∥OC.
∵Q是OB的中点,
∴BH=CH=
 BC.
BC.∵∠NQM=90°,
∴∠NQD=∠MQH,
∵∠QND+∠NQD=45°,∠MQH+∠QMH=45°
∴∠QND=∠QMH,
∴△QHM∽△QDN,
∴
 ,
,∴HM=
 ND,
ND,∵BM-HM=HB,
∴
 .
.故答案为:

(3)∵MB:MC=3:1,设CM=x,
∴MB=3x,
∴CB=CD=4x,
∴PB=2x,
∴PM=x.
∵HM=
 ND,
ND,∴ND=3x,
∴CN=7x
∵四边形ABCD是正方形,
∴ED∥BC,
∴△NDE∽△NCM,△DEF∽△BMF,
∴
 ,
, ,
,∴
 ,
,
∴DE=
 ,
,∴

∵NQ=
 ,
,∴QM=3
 ,
,在Rt△MNQ中,由勾股定理得:
MN=
 =15
=15 .
.∴
 ,
,∴NE=

∴EM=

设EF=a,则FM=7a,
∴a+7a=

∴a=

点评:本题是一道相似的综合试题,考查了正方形的性质的运用,相似三角形的判定于性质的运用,勾股定理的运用及平行线等分线段定理的运用,在解答时利用三角形相似的性质求出线段的比是解答本题的关键.

练习册系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.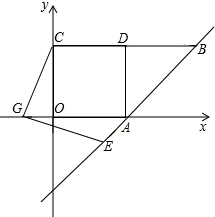



 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.