Question

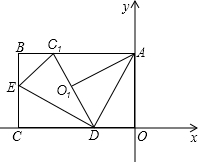如图，已知平面直角坐标系中，有一矩形纸片OABC，O为坐标原点，AB∥x轴，B（-3，

3

），现将纸片按如图折叠，AD，DE为折痕，∠OAD=30°．折叠后，点O落在点O₁，点C落在线段AB上的C₁处，并且DO₁与DC₁在同一直线上．则C₁的坐标是

（-2，

3

）

．

Answer 1

分析：可过C₁作x轴的垂线，由于∠ADO=∠AOC₁=60°，因此可得出∠C₁DC=60°，因此可在构建的直角三角形中用BC的长和∠C₁DC的度数来求出C₁的坐标．

解答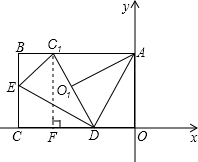：解：过C₁作C₁F⊥OC于点F，
∵∠OAD=30°，
∴∠ADO=∠ADO₁=60°，
∴∠C₁DC=60°，
∵B（-3，

3

），
∴AO=BC=

3

，AB=CO=3，
∴tan60°=

AO

DO

=

3

，
∴DO=1，
∴DC=3-1=2，
∴DC₁=DC=2，
∴在Rt△C₁DF中，C₁F=DC₁•sin∠C₁DF=2×sin60°=

3

．
则DF=

1

2

DC₁=1，
∴C₁（-2，

3

），
故答案为：（-2，

3

）．

点评：此题主要考查了翻折变换的性质以及等腰直角三角形的性质以及三角形中位线的性质等知识，根据已知得出BF的长是解题关键．