题目内容
如图AC、BC是△AOB的两个外角∠MAB和∠NBA的平分线，C为交点，已知，∠AOB=50°，
则∠COB=________度．
25
分析：首先过点C作CE⊥ON于E，CF⊥AB于F，CG⊥OM于G，由AC、BC是△AOB的两个外角∠MAB和∠NBA的平分线，根据角平分线的性质，即可证得CE=CG，由角平分线的判定，可得OC是∠AOB的角平分线，则可求得∠COB的度数．
解答：
解：过点C作CE⊥ON于E，CF⊥AB于F，CG⊥OM于G，
∵AC、BC是△AOB的两个外角∠MAB和∠NBA的平分线，
∴CE=CF，CF=CG
∴CE=CG，
∴OC是∠AOB的角平分线，
∴∠COB=
∠AOB=×50°=25°．
故答案为：25．
点评：此题考查角平分线的性质与判定．此题难度不大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
分析：首先过点C作CE⊥ON于E，CF⊥AB于F，CG⊥OM于G，由AC、BC是△AOB的两个外角∠MAB和∠NBA的平分线，根据角平分线的性质，即可证得CE=CG，由角平分线的判定，可得OC是∠AOB的角平分线，则可求得∠COB的度数．
解答：
解：过点C作CE⊥ON于E，CF⊥AB于F，CG⊥OM于G，∵AC、BC是△AOB的两个外角∠MAB和∠NBA的平分线，
∴CE=CF，CF=CG
∴CE=CG，
∴OC是∠AOB的角平分线，
∴∠COB=
∠AOB=×50°=25°．故答案为：25．
点评：此题考查角平分线的性质与判定．此题难度不大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
练习册系列答案
阅读快车系列答案
相关题目
如图AC、BC是△AOB的两个外角∠MAB和∠NBA的平分线，C为交点，已知，∠AOB=50°，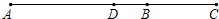
已知AB=10cm，点C在直线AB上，如果BC=4cm，点D是线段AC的中点，求线段BD的长度．
已知AB=10cm，点C在直线AB上，如果BC=4cm，点D是线段AC的中点，求线段BD的长度．
A
于D.