题目内容
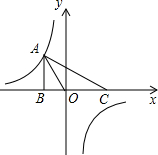 (2013•黑龙江)如图,Rt△ABC的顶点A在双曲线y=
(2013•黑龙江)如图,Rt△ABC的顶点A在双曲线y=| k |
| x |
分析:根据三角形外角性质得∠OAC=∠AOB-∠ACB=30°,易得OA=OC=4,然后再Rt△AOB中利用含30度的直角三角形三边的关系得到OB=
OC=2,AB=
OB=2
,则可确定A点坐标为(-2,2
),最后把A点坐标代入反比例函数解析式y=
中即可得到k的值.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| k |
| x |
解答:解:∵∠ACB=30°,∠AOB=60°,
∴∠OAC=∠AOB-∠ACB=30°,
∴∠OAC=∠ACO,
∴OA=OC=4,
在△AOB中,∠ABC=90°,∠AOB=60°,OA=4,
∴∠OAB=30°,
∴OB=
OC=2,
∴AB=
OB=2
,
∴A点坐标为(-2,2
),
把A(-2,2
)代入y=
得k=-2×2
=-4
.
故选B.
∴∠OAC=∠AOB-∠ACB=30°,
∴∠OAC=∠ACO,
∴OA=OC=4,
在△AOB中,∠ABC=90°,∠AOB=60°,OA=4,
∴∠OAB=30°,
∴OB=
| 1 |
| 2 |
∴AB=
| 3 |
| 3 |
∴A点坐标为(-2,2
| 3 |
把A(-2,2
| 3 |
| k |
| x |
| 3 |
| 3 |
故选B.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征;熟练运用含30度的直角三角形三边的关系进行几何计算.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 (2013•黑龙江)如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件:
(2013•黑龙江)如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: