题目内容
如图,?ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于N,若DN=4,∠ADB=30°,那么BN= .
【答案】分析:作AE⊥BD.BN=BE-NE,解直角三角形分别求BE、NE的长.
解答: 解:如图,作AE⊥BD.
解:如图,作AE⊥BD.
∵AD∥BC,
∴∠BDC=∠ADB=30°,
∴∠AND=60°,∠ABE=∠ABC-∠DBC=75°-30°=45°,
∴∠BAE=∠ABE=45°,
∴AE=BE,
∵AD=DNcos30°=2 ,BE=AE=ADsin30°=
,BE=AE=ADsin30°=
∴NE=AEcot60°=1.
BN=BE-EN= -1
-1
点评:本题考查了平行四边形的性质和锐角三角函数的概念及等角对等边求解.
解答:
 解:如图,作AE⊥BD.
解:如图,作AE⊥BD.∵AD∥BC,
∴∠BDC=∠ADB=30°,
∴∠AND=60°,∠ABE=∠ABC-∠DBC=75°-30°=45°,
∴∠BAE=∠ABE=45°,
∴AE=BE,
∵AD=DNcos30°=2
 ,BE=AE=ADsin30°=
,BE=AE=ADsin30°=
∴NE=AEcot60°=1.
BN=BE-EN=
 -1
-1点评:本题考查了平行四边形的性质和锐角三角函数的概念及等角对等边求解.

练习册系列答案
相关题目
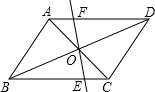 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
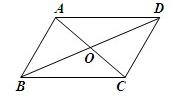 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )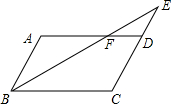 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=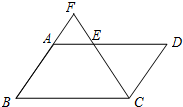 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为