题目内容
已知不等式ax2+bx+c>0的x的取值范围是x<1或x>3,则满足不等式cx2+bx+a>0的x的取值范围是
- A.

- B.x<-1或x>3
- C.x<-3或x>-1
- D.

A
分析:由不等式ax2+bx+c>0的x的取值范围是x<1或x>3,根据y=ax2+bx+c(a≠0)的图象得到y=a(x-1)(x-3),所以不等式ax2+bx+c>0可变形为不等式(x-1)(x-3)>0,即x2-4x+3>0,则不等式cx2+bx+a>0可变形为3x2-4x+1>0,即(3x-1)(x-1)>0,再通过y=c(3x-1)(x-1)的图象得到它的解集.
解答:∵不等式ax2+bx+c>0的x的取值范围是x<1或x>3,
∴不等式ax2+bx+c>0可变形为不等式(x-1)(x-3)>0,即x2-4x+3>0,
∴不等式cx2+bx+a>0可变形为3x2-4x+1>0,即(3x-1)(x-1)>0,解得x< 或x>1,
或x>1,
∴满足不等式cx2+bx+a>0的x的取值范围为x< 或x>1.
或x>1.
故选A.
点评:本题考查了二次函数与不等式组的关系:通过二次函数y=ax2+bx+c(a≠0)的图象可得到ax2+bx+c>0的解集,即找到抛物线在x轴上方所对应的x的范围.
分析:由不等式ax2+bx+c>0的x的取值范围是x<1或x>3,根据y=ax2+bx+c(a≠0)的图象得到y=a(x-1)(x-3),所以不等式ax2+bx+c>0可变形为不等式(x-1)(x-3)>0,即x2-4x+3>0,则不等式cx2+bx+a>0可变形为3x2-4x+1>0,即(3x-1)(x-1)>0,再通过y=c(3x-1)(x-1)的图象得到它的解集.
解答:∵不等式ax2+bx+c>0的x的取值范围是x<1或x>3,
∴不等式ax2+bx+c>0可变形为不等式(x-1)(x-3)>0,即x2-4x+3>0,
∴不等式cx2+bx+a>0可变形为3x2-4x+1>0,即(3x-1)(x-1)>0,解得x<
 或x>1,
或x>1,∴满足不等式cx2+bx+a>0的x的取值范围为x<
 或x>1.
或x>1.故选A.
点评:本题考查了二次函数与不等式组的关系:通过二次函数y=ax2+bx+c(a≠0)的图象可得到ax2+bx+c>0的解集,即找到抛物线在x轴上方所对应的x的范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知不等式ax2+bx+c>0的x的取值范围是x<1或x>3,则满足不等式cx2+bx+a>0的x的取值范围是( )
A、x<
| ||
| B、x<-1或x>3 | ||
| C、x<-3或x>-1 | ||
D、x<-1或x>-
|
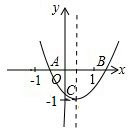 已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①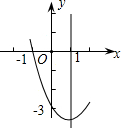 已知抛物线y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
已知抛物线y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
