题目内容
5. 如图,在直角三角形ABC中,∠ACB=90°,AC=1,BC=2,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{2\sqrt{5}}{5}$.
如图,在直角三角形ABC中,∠ACB=90°,AC=1,BC=2,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{2\sqrt{5}}{5}$.
分析 作CE⊥AB于E,根据勾股定理得到AB=$\sqrt{5}$,利用三角形面积公式求出CE,根据勾股定理求出AE,根据垂径定理计算即可.
解答 解: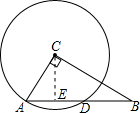 作CE⊥AB于E,
作CE⊥AB于E,
则AE=$\frac{1}{2}$AD,
∵∠ACB=90°,AC=1,BC=2,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$,
$\frac{1}{2}$×AB×CE=$\frac{1}{2}×$AC×BC,即$\frac{1}{2}×$$\sqrt{5}$×CE=$\frac{1}{2}×1×2$,
解得,CE=$\frac{2\sqrt{5}}{5}$,
AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\frac{\sqrt{5}}{5}$,
则AD=2AE=$\frac{2\sqrt{5}}{5}$,
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查的是勾股定理和垂径定理的应用,垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
13.已知x=2是方程2x+a=1的解,则a的值是( )
| A. | 3 | B. | 4 | C. | -5 | D. | -3 |
10. 假设如图的方格纸中,每个小正方形的面积是2,则图中的四条线段中,长度是无理数的有( )条.
假设如图的方格纸中,每个小正方形的面积是2,则图中的四条线段中,长度是无理数的有( )条.
 假设如图的方格纸中,每个小正方形的面积是2,则图中的四条线段中,长度是无理数的有( )条.
假设如图的方格纸中,每个小正方形的面积是2,则图中的四条线段中,长度是无理数的有( )条.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |