题目内容
已知:⊙O的面积为4π,△ABC内接于⊙O,a、b、c分别是三角形三个内角∠A、∠B、∠C的对边的长,关于x的方程(a+c)x2-2bx+c-a=0有两个相等的实数根,cosA,cosB是二次函数y=[m-( )]x2-[m+(
)]x2-[m+( )]x+
)]x+ 的图象与x轴的两个交点的横坐标.求△ABC三边的长.
的图象与x轴的两个交点的横坐标.求△ABC三边的长.
解:∵关于x的方程(a+c)x2-2bx+c-a=0有两个相等的实数根,
∴(-2b)2-4(a+c)(c-a)=0,
整理,得a2+b2=c2,
∴△ABC是直角三角形,∠C=90°,
∴∠A+∠B=90°,
∴sinA=cosB.
∵cosA,cosB是二次函数y=[m-( )]x2-[m+(
)]x2-[m+( )]x+
)]x+ 的图象与x轴的两个交点的横坐标,
的图象与x轴的两个交点的横坐标,
∴sinA、cosA是关于x的方程[m-( )]x2-[m+(
)]x2-[m+( )]x+
)]x+ =0的两个根,
=0的两个根,
∴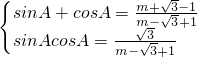 ,
,
又∵sin2A+cos2A=1,
∴(sinA+cosA)2-2sinA•cosA=1,
∴(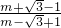 )2-2×
)2-2×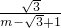 =1,
=1,
整理,得(4-2 )m=6-2
)m=6-2 ,
,
解得m=3+ ,
,
经检验,m=3+ 是原方程的根,
是原方程的根,
当m=3+ 时,原方程变为4x2-(2+2
时,原方程变为4x2-(2+2 )x+
)x+ =0,
=0,
解得x1= ,x2=
,x2= ,
,
∵△ABC的外接圆面积为4π,
∴外接圆半径R=2,
∴斜边c=4.
∴另外两直角边为2,2 .
.
分析:先由关于x的方程(a+c)x2-2bx+c-a=0有两个相等的实数根,得到判别式△=0,进而得到a2+b2=c2,根据勾股定理的逆定理判定△ABC是直角三角形,再利用互余两角三角函数之间的关系得到sinA=cosB,再根据一元二次方程根与系数的关系及同角三角函数之间的关系求得m的值;将m的值代入方程[m-( )]x2-[m+(
)]x2-[m+( )]x+
)]x+ =0,解方程求出x的值,由圆的面积公式求出△ABC的外接圆半径R,得到斜边为2R,进而求得两直角边的长度.
=0,解方程求出x的值,由圆的面积公式求出△ABC的外接圆半径R,得到斜边为2R,进而求得两直角边的长度.
点评:本题考查了二次函数的性质,勾股定理的逆定理,互余两角、同角的三角函数之间的关系,一元二次方程根与系数的关系,综合性较强,难度适中.
∴(-2b)2-4(a+c)(c-a)=0,
整理,得a2+b2=c2,
∴△ABC是直角三角形,∠C=90°,
∴∠A+∠B=90°,
∴sinA=cosB.
∵cosA,cosB是二次函数y=[m-(
 )]x2-[m+(
)]x2-[m+( )]x+
)]x+ 的图象与x轴的两个交点的横坐标,
的图象与x轴的两个交点的横坐标,∴sinA、cosA是关于x的方程[m-(
 )]x2-[m+(
)]x2-[m+( )]x+
)]x+ =0的两个根,
=0的两个根,∴
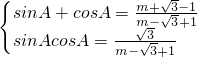 ,
,又∵sin2A+cos2A=1,
∴(sinA+cosA)2-2sinA•cosA=1,
∴(
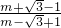 )2-2×
)2-2×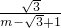 =1,
=1,整理,得(4-2
 )m=6-2
)m=6-2 ,
,解得m=3+
 ,
,经检验,m=3+
 是原方程的根,
是原方程的根,当m=3+
 时,原方程变为4x2-(2+2
时,原方程变为4x2-(2+2 )x+
)x+ =0,
=0,解得x1=
 ,x2=
,x2= ,
,∵△ABC的外接圆面积为4π,
∴外接圆半径R=2,
∴斜边c=4.
∴另外两直角边为2,2
 .
.分析:先由关于x的方程(a+c)x2-2bx+c-a=0有两个相等的实数根,得到判别式△=0,进而得到a2+b2=c2,根据勾股定理的逆定理判定△ABC是直角三角形,再利用互余两角三角函数之间的关系得到sinA=cosB,再根据一元二次方程根与系数的关系及同角三角函数之间的关系求得m的值;将m的值代入方程[m-(
 )]x2-[m+(
)]x2-[m+( )]x+
)]x+ =0,解方程求出x的值,由圆的面积公式求出△ABC的外接圆半径R,得到斜边为2R,进而求得两直角边的长度.
=0,解方程求出x的值,由圆的面积公式求出△ABC的外接圆半径R,得到斜边为2R,进而求得两直角边的长度.点评:本题考查了二次函数的性质,勾股定理的逆定理,互余两角、同角的三角函数之间的关系,一元二次方程根与系数的关系,综合性较强,难度适中.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
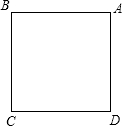 如图,已知正方形ABCD的面积为S.
如图,已知正方形ABCD的面积为S. 如图,在直角坐标系中,已知菱形ABCD的面积为5,顶点A在双曲线
如图,在直角坐标系中,已知菱形ABCD的面积为5,顶点A在双曲线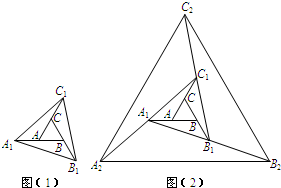 (2011•成华区二模)如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为
(2011•成华区二模)如图(1),已知正△ABC的面积为1,把它的各边延长一倍得到正△A1B1C1;再把△A1B1C1的各边延长一倍得到正△A2B2C2(如(2));…;如此下去,则正△AnBnCn的面积为