题目内容
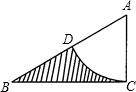 已知:如图,Rt△ABC中,∠C=90°,∠B=30°,
已知:如图,Rt△ABC中,∠C=90°,∠B=30°,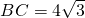 ,以A点为圆心,AC长为半径作
,以A点为圆心,AC长为半径作 ,求∠B与
,求∠B与 围成的阴影部分的面积.
围成的阴影部分的面积.
解:∵Rt△ABC中,∠C=90°,∠B=30°,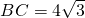 ,
,
∴AC=BC•tan∠B=4 ×
× =4,
=4,
∴∠A=90°-∠B=90°-30°=60°,
∴S阴影=S△ABC-S扇形ACD= AC•BC-
AC•BC-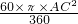 =
= ×4×4
×4×4 -
-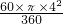 =8
=8 -
-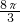 .
.
答:阴影部分的面积为:8 -
-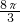 .
.
分析:先根据锐角三角函数的定义求出BC的长,再由直角三角形的性质求出∠A的度数,再根据S阴影=S△ABC-S扇形ACD进行计算即可.
点评:本题考查的是扇形面积的计算及直角三角形的性质,熟知三角形及扇形的面积公式是解答此题的关键.
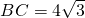 ,
,∴AC=BC•tan∠B=4
 ×
× =4,
=4,∴∠A=90°-∠B=90°-30°=60°,
∴S阴影=S△ABC-S扇形ACD=
 AC•BC-
AC•BC-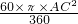 =
= ×4×4
×4×4 -
-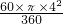 =8
=8 -
-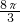 .
.答:阴影部分的面积为:8
 -
-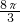 .
.分析:先根据锐角三角函数的定义求出BC的长,再由直角三角形的性质求出∠A的度数,再根据S阴影=S△ABC-S扇形ACD进行计算即可.
点评:本题考查的是扇形面积的计算及直角三角形的性质,熟知三角形及扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
 22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明.
22、已知:如图,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有字母的点为端点,连接两条线段,如果你所连接的两条线段满足相等,垂直或平行关系中的一种,那么请你把它写出来并证明. 20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.
20、已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A、B两点重合,AE⊥AB,AE=BD,连接DE、DC.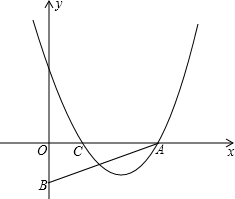 C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.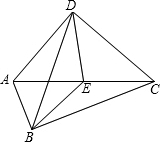 已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.
已知:如图,Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,点E是AC的中点.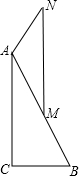 已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.
已知:如图,Rt△ABC中,∠C=90°,M是AB的中点,AM=AN,MN∥AC.