题目内容
 如图,△ABC中,AB=BC,∠ABC=90°,点D在CB的延长线上,点E在AB上,且DB=EB.
如图,△ABC中,AB=BC,∠ABC=90°,点D在CB的延长线上,点E在AB上,且DB=EB.(1)求证:CE⊥AD;
(2)当∠ACE=30°时,求∠DAC的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)延长CE交AD于点F,先根据SAS定理得出△CBE与△ABD,故可得出∠CEB=∠ADB,所以∠BCE+∠ADB=∠BCE+∠CEB=90°,由此可得出结论;
(2)先根据AB=BC,∠ABC=90°,得出∠BAC=∠ACB=45°,故可得出∠BCE=15°,由(1)知,Rt△CBE≌Rt△ABD,所以∠DAE=15°,根据∠DAC=∠DAE+∠BAC即可得出结论.
(2)先根据AB=BC,∠ABC=90°,得出∠BAC=∠ACB=45°,故可得出∠BCE=15°,由(1)知,Rt△CBE≌Rt△ABD,所以∠DAE=15°,根据∠DAC=∠DAE+∠BAC即可得出结论.
解答: (1)证明:延长CE交AD于点F,
(1)证明:延长CE交AD于点F,
在△CBE与△ABD中,
∵
,
∴△CBE≌△ABD(SAS),
∴∠CEB=∠ADB,
∴∠BCE+∠ADB=∠BCE+∠CEB=90°,
∴CE⊥AD;
(2)解:∵AB=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵∠ACE=30°,
∴∠BCE=45°-30°=15°,
∵由(1)知,Rt△CBE≌Rt△ABD,
∴∠DAE=15°,
∴∠DAC=∠DAE+∠BAC=15°+45°=60°.
 (1)证明:延长CE交AD于点F,
(1)证明:延长CE交AD于点F,在△CBE与△ABD中,
∵
|
∴△CBE≌△ABD(SAS),
∴∠CEB=∠ADB,
∴∠BCE+∠ADB=∠BCE+∠CEB=90°,
∴CE⊥AD;
(2)解:∵AB=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵∠ACE=30°,
∴∠BCE=45°-30°=15°,
∵由(1)知,Rt△CBE≌Rt△ABD,
∴∠DAE=15°,
∴∠DAC=∠DAE+∠BAC=15°+45°=60°.
点评:本题考查的是全等三角形的判定与性质,熟知SAS,ASA,SSS,HL等判定定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


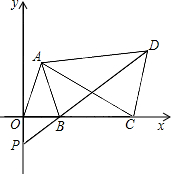 如图,平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且
如图,平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且