题目内容
已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是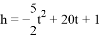
.若此礼炮在升空到最高处时引爆，则引爆需要的时间为_______.
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
小学教材全测系列答案小学数学口算题卡脱口而出系列答案优秀生应用题卡口算天天练系列答案浙江之星课时优化作业系列答案题目内容
已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是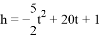.若此礼炮在升空到最高处时引爆，则引爆需要的时间为_______.
小学教材全测系列答案小学数学口算题卡脱口而出系列答案优秀生应用题卡口算天天练系列答案浙江之星课时优化作业系列答案
是整数，则正整数n的最小值是（ ）
和一次函数
．
的图象与x轴是否有公共点，如果有，请写出公共点的坐标；
的图象与x轴的两个不同公共点，且这两个公共点间的距离为8，求t的值；
≥
．
B. 
C. 
D. 