题目内容
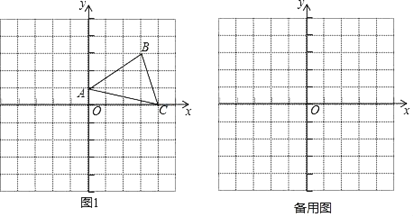
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求出![]() ,利用翻折不变性解决问题即可.
,利用翻折不变性解决问题即可.
(2)如图2中,作BH⊥AD于H.根据30度角所对的直角边等于斜边的一半及勾股定理求出AH,PH即可解决问题.
(3)![]() 的周长=
的周长=![]() +BF+
+BF+![]() =AF+BF+
=AF+BF+![]() =AB+
=AB+![]() =10+
=10+![]() ,推出当
,推出当![]() 的周长最小时,
的周长最小时,![]() 的周长最小,由此即可解决问题.
的周长最小,由此即可解决问题.
(1)如图1:
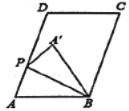
图1
∵![]()
∴![]()
由折叠的性质可知:
![]()
故答案为:![]()
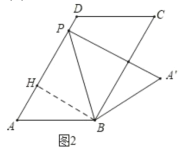
(2)如图2:作BH⊥AD于H
在Rt△ABH中
∵∠AHB=![]() ,AB=10,
,AB=10,![]()
∴∠ABH=![]()
∴AH=![]() AB=5
AB=5
![]() BH=
BH=![]()
∵四边形ABCD是平行四边形
∴AD∥BC
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
故答案为:![]()
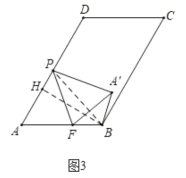
(3)如图3中,作BH⊥AD于H ,连接BP
∵PA=8,AH=5
∴PH=3
∵BH=![]()
∴PB=![]()
由翻折可知:PA=![]() =8,FA=
=8,FA=![]() ,
,
![]() 的周长
的周长
![]() +BF+
+BF+![]() =AF+BF+
=AF+BF+![]() =AB+
=AB+![]() =10+
=10+![]()
∴当![]() 最小时,
最小时, ![]() 的周长最小
的周长最小
∵![]()
∴![]()
∴![]() 的最小值为
的最小值为![]()
∴![]() 的周长的最小值为:
的周长的最小值为: ![]()
故答案为:![]()

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目