Question

【题目】抛物线交轴于，两点（点在点的左边），交轴正半轴于点.

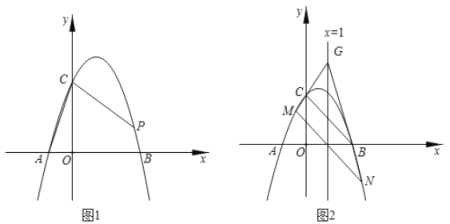
（1）如图1，当时.

①直接写出点，，的坐标；

②若抛物线上有一点，使，求点的坐标.

（2）如图2，平移直线交抛物线于，两点，直线与直线交于点，若点在定直线上运动，求的值.

Answer 1

【答案】（1）①，，；②；（2）

【解析】

（1）①令x=0，可求点C坐标，令y=0，可求A点，B点坐标；
②延长CP交x轴于点E，由勾股定理和等腰三角形的性质可求点Q坐标，再求直线CE的解析式，联立方程可求点P坐标；（2）先求出BC解析式，再求出点M，N的横坐标，最后利用联立可解决问题．

（1）①当m=3时，y=-x2+2x+3，

当x=0时，y=3，则点C（0，3），

当y=0时，0=-x2+2x+3，

∴x1=3，x2=-1，

∴，，；

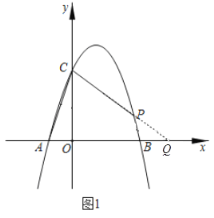
②如图1，延长交轴于点，设，

∵，

∴，

∴，

在中，，

∴，

解得，

∴，

∴直线的解析式为，

联立，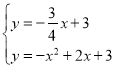

∴，

∴（舍），

∵在抛物线上，

∴；

（2）如图2，

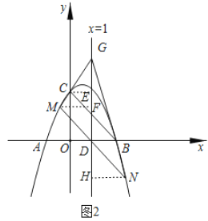
令，，，

∴，，，

设解析式为：，

联立 ，即 ，

∴，

同理：设解析式为：，

∴，

∵，

∴的解析式为，

∴设解析式为：，

联立，

∴，

∴，

∴即，

联立，

∴，

∴，

又，

∴，

∴.