Question

已知：在面积为7的梯形ABCD中，AD∥BC，AD=3，BC=4，P为边AD上不与A、D重合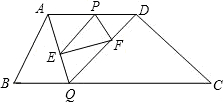的一动点，Q是边BC上的任意一点，连接AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F，则△PEF面积最大值是

 

．

Answer 1

分析：设PD=x，S_△PEF=y．根据平行线的性质、全等三角形的判定及相似三角形的判定，证明△PEF≌△QFE、△AEP∽△AQD、△PDF∽△ADQ，相似三角形的面积比是相似比的平方，再由三角形AQD与梯形ABCD的面积公式求得梯形的高，代入S_△PEF=（S_△AQD-S_△DPF-S_△APE）÷2，得出关于x的二次函数方程，根据顶点坐标公式，求得则△PEF面积最大值．

解答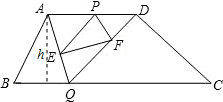：解：设PD=x，S_△PEF=y，S_△AQD=z，梯形ABCD的高为h，
∵AD=3，BC=4，梯形ABCD面积为7，
∴

z= 1 2 ×3×h 7= 1 2 (3+4)h

解得

h=2 z=3

∵PE∥DQ，
∴∠PEF=∠QFE，∠EPF=∠PFD，
又∵PF∥AQ，
∴∠PFD=∠EQF，
∴∠EPF=∠EQF，
∵EF=FE，
∴△PEF≌△QFE（AAS），
∵PE∥DQ，
∴△AEP∽△AQD，
同理，△DPF∽△DAQ，
∴

S△AEP

S△AQD

=(

3-x

3

)2，

S△DPF

S△DAQ

=（

x

3

）²，
∵S_△AQD=3，∴S_△DPF=

1

3

x²，
S_△APE=

1

3

（3-x）²，
∴S_△PEF=（S_△AQD-S_△DPF-S_△APE）÷2，
∴y=[3-

1

3

x²-

1

3

（3-x）²]×

1

2

=-

1

3

x²+x，
∵y_最大值=

0-12

4×(- 1 3 )

=

3

4

，即y_最大值=

3

4

．
∴△PEF面积最大值是

3

4

．

点评：本题综合考查了二次函数的最值、三角形的面积、梯形的面积以及相似三角形的判定与性质．