��Ŀ����
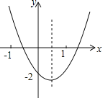
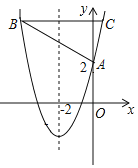
����Ŀ����ƽ��ֱ������ϵ�У����Ƕ���ֱ��y=ax-aΪ������y=ax2+bx+c��a��b��cΪ������a��0����������ֱ��������һ���������������ϣ�����һ��������y���ϵ�������Ϊ��������������������֪������![]() ����������ֱ��������A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
����������ֱ��������A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
��1����գ��������ߵ�������ֱ�����Ľ���ʽΪ ����A������Ϊ ����B������Ϊ ��
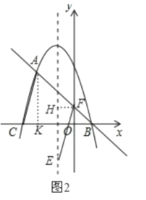
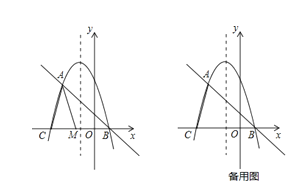
��2����ͼ����MΪ�߶�CB��һ���㣬����ACM��AM����ֱ��Ϊ�Գ��ᷭ�ۣ���C�ĶԳƵ�ΪN������AMNΪ�������ߵ��������������������N�����ꣻ
��3������E�������ߵĶԳ������˶�ʱ���ڸ������ߵ�������ֱ�����ϣ��Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����-2��
����-2��![]() ������1,0����
������1,0����
��2��N���������0��![]() ������0��
������0��![]() ����
����
��3��E��-1��-![]() ����F��0��
����F��0��![]() ����E��-1��
����E��-1��![]() ����F��-4��
����F��-4��![]() ��
��
��������
��1���������ߵ�������ֱ����֪�����κ�������ʽ��a���ɣ���2����A��AD��y���ڵ�D�����֪AN=AC�����A�����꣬������ON�ij��������N������ꣻ��3���ֱ����۵�ACΪƽ���ı��εı�ʱ����ACΪƽ���ı��εĶԽ���ʱ���������������E��F���꼴��
��1����![]() ��a=
��a=![]() ���������ߵ�������ֱ�����Ľ���ʽΪ
���������ߵ�������ֱ�����Ľ���ʽΪ![]() ��
��
����������ʽ��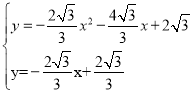 �����
�����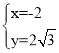 ��
��![]() ��
��
��A��-2��![]() ����B��1,0����
����B��1,0����
��2����ͼ1����A��AD��y���ڵ�D��
��![]() ����y=0�����x= -3��x=1��
����y=0�����x= -3��x=1��
��C��-3,0������A��-2��![]() ����
����
��AC=![]()
�ɷ��۵����ʿ�֪AN=AC=![]() ��
��
����AMNΪ�������ߵ�����������������
��N��y���ϣ���AD=2��
��Rt��AND�У��ɹ��ɶ����ɵ�
DN=![]() ��
��
��OD=![]() ��
��
��ON=![]() ��ON=
��ON=![]() ��
��
��N���������0��![]() ������0��
������0��![]() ����
����
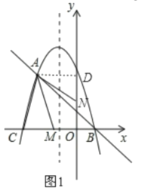
��3���ٵ�ACΪƽ���ı��εı�ʱ����ͼ2 ����F���Գ���Ĵ���FH����A��AK��x���ڵ�K������AC��EF��AC=EF��
���� ACK=�� EFH��
���� ACK���� EFH��
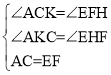
���� ACK�ա� EFH��
��FH=CK=1��HE=AK=![]() ��
��
�������ߵĶԳ���Ϊx=-1��
�� F��ĺ�����Ϊ0��-2��
�ߵ�F��ֱ��AB�ϣ�
�൱F��ĺ�����Ϊ0ʱ����F��0��![]() ������ʱ��E��ֱ��AB�·���
������ʱ��E��ֱ��AB�·���
��E��y��ľ���ΪEH-OF=![]() -
-![]() =
=![]() ����E��������Ϊ-
����E��������Ϊ-![]() ��
��
�� E��-1��-![]() ����
����
��F��ĺ�����Ϊ-2ʱ����F��A�غϣ��������⣬��ȥ��
����ACΪƽ���ı��εĶԽ���ʱ��
�� C��-3,0������A��-2��![]() ����
����
���߶�AC���е�����Ϊ��-2.5�� ![]() ����
����
��E��-1��t����F��x��y����
��x-1=2����-2.5����y+t=![]() ��
��
��x= -4��y=![]() -t��
-t��
![]() -t=-
-t=-![]() ����-4��+
����-4��+![]() �����t=
�����t=![]() ��
��
��E��-1��![]() ����F��-4��
����F��-4��![]() ����
����
���Ͽ�֪�������������ĵ�F����ʱE��-1��-![]() ������0��
������0��![]() ����E��-1��
����E��-1��![]() ����F��-4��
����F��-4��![]() ��
��