题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() .
.
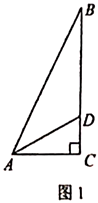
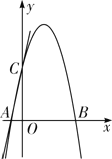
(1)如图1,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
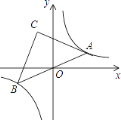
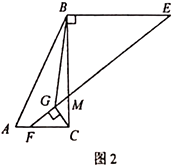
(2)如图2,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
【答案】(1)3;(2)见解析.
【解析】
(1)根据勾股定理可得AC,进而可得BC与BD,然后根据三角形的面积公式计算即可;
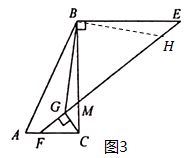
(2)过点B作BH⊥BG交EF于点H,如图3,则根据余角的性质可得∠CBG=∠EBH,由已知易得BE∥AC,于是∠E=∠EFC,由于![]() ,
,![]() ,则根据余角的性质得∠EFC=∠BCG,于是可得∠E=∠BCG,然后根据ASA可证△BCG≌△BEH,可得BG=BH,CG=EH,从而△BGH是等腰直角三角形,进一步即可证得结论.
,则根据余角的性质得∠EFC=∠BCG,于是可得∠E=∠BCG,然后根据ASA可证△BCG≌△BEH,可得BG=BH,CG=EH,从而△BGH是等腰直角三角形,进一步即可证得结论.
解:(1)在△ACD中,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴BC=4,BD=3,∴
,∴BC=4,BD=3,∴![]() ;
;
(2)过点B作BH⊥BG交EF于点H,如图3,则∠CBG+∠CBH=90°,
∵![]() ,∴∠EBH+∠CBH=90°,∴∠CBG=∠EBH,
,∴∠EBH+∠CBH=90°,∴∠CBG=∠EBH,
∵![]() ,
,![]() ,∴BE∥AC,∴∠E=∠EFC,
,∴BE∥AC,∴∠E=∠EFC,
∵![]() ,
,![]() ,∴∠EFC+∠FCG=90°,∠BCG+∠FCG=90°,
,∴∠EFC+∠FCG=90°,∠BCG+∠FCG=90°,
∴∠EFC=∠BCG,∴∠E=∠BCG,
在△BCG和△BEH中,∵∠CBG=∠EBH,BC=BE,∠BCG=∠E,∴△BCG≌△BEH(ASA),
∴BG=BH,CG=EH,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目