题目内容
（2013•抚顺）如图，等边△OAB的边OB在x轴的负半轴上，双曲线y=| k |
| x |
分析：如图，过点C作CD⊥OB于点D．根据等边三角形的性质、中点的定义可以求得点C的坐标，然后把点C的坐标代入双曲线方程，列出关于系数k的方程，通过解该方程即可求得k的值．
解答：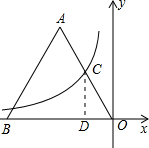
解：如图，过点C作CD⊥OB于点D．
∵△OAB是等边三角形，该等边三角形的边长是4，
∴OA=4，∠COD=60°，
又∵点C是边OA的中点，
∴OC=2，
∴OD=OC•cos60°=2×
=1，CD=OC•sin60°=2×
=
．
∴C（-1，
）．
则
=
，
解得，k=-
，
∴该双曲线的表达式为y=-
．
故选B．
解：如图，过点C作CD⊥OB于点D．∵△OAB是等边三角形，该等边三角形的边长是4，
∴OA=4，∠COD=60°，
又∵点C是边OA的中点，
∴OC=2，
∴OD=OC•cos60°=2×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴C（-1，
| 3 |
则
| 3 |
| k |
| -1 |
解得，k=-
| 3 |
∴该双曲线的表达式为y=-
| ||
| x |
故选B．
点评：本题考查了待定系数法求反比例函数解析式，等边三角形的性质．解题的关键是求得点C的坐标．
练习册系列答案
相关题目
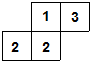（2013•抚顺）如图是由八个小正方形搭成的几何体的俯视图，小正方形中的数字表示该位置上的小正方体的个数，则这个几何体的左视图是（ ）
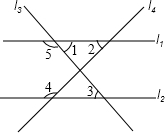（2013•抚顺）如图，直线l1、l2被直线l3、l4所截，下列条件中，不能判断直线l1∥l2的是（ ）
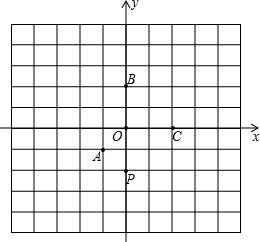（2013•抚顺）如图，在平面直角坐标系中，点A、B、C的坐标分别是（-1，-1）、（0，2）、（2，0），点P在y轴上，且坐标为（0，-2）．点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，点P4关于点B的对称点为P5，点P5关于点C的对称点为P6，点P6关于点A的对称点为P7…，按此规律进行下去，则点P2013的坐标、是
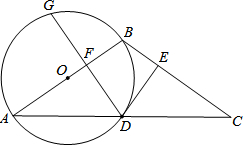（2013•抚顺）如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，DE⊥BC，垂足为E．