题目内容
如图，一只小蚂蚁要从A点沿长方体木块表面爬到B点处吃蜜糖．已知长方体木块的长、宽、高分别为10cm、8cm、6cm，试计算小蚂蚁爬行的最短距离．分析：根据题意画出不同数值的三种情况，根据勾股定理求出每种情况的AB，再比较即可．
解答：解：
展开后有三种不同的情况如图，
如图1，AB=
=
，
如图2，AB=
=
，
如图3，AB=
=
，
∵
＜
＜
，
∴小蚂蚁爬行的最短路线为
cm．
展开后有三种不同的情况如图，
如图1，AB=
| (10+8)2+62 |
| 360 |
如图2，AB=
| 102+(6+8)2 |
| 296 |
如图3，AB=
| 82+(10+6)2 |
| 320 |
∵
| 296 |
| 320 |
| 360 |
∴小蚂蚁爬行的最短路线为
| 296 |
点评：本题考查了平面展开-最短路线问题，勾股定理的应用，主要考查学生能否求出符合条件的所有情况．
练习册系列答案
相关题目
如图所示一棱长为3cm的正方体，把所有的面均分成3×3个小正方形．其边长都为1cm，假设一只蚂蚁每秒爬行2cm，则它从下底面点A沿表面爬行至侧面的B点，最少要用
的正方体，把所有面都分为
个小正方形，其边 长都是
，假设一只蚂蚁每秒爬行
，则它从下底面
点沿表面爬行至右侧面的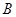
点，最少要花____________秒钟.
的正方体，把所有面都分为
个小正方形，其边 长都是
，假设一只蚂蚁每秒爬行
，则它从下底面
点沿表面爬行至右侧面的
点，最少要花____________秒钟.
