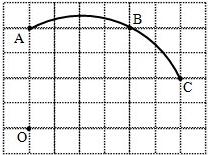
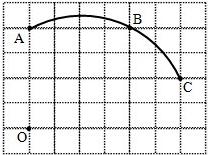
题目内容
如图,AD是圆O的直径,BC切圆O于点D,AB,AC与圆O相交于点E,F.求证:AE•AB=AF•AC.
【答案】分析:连接DE,证明Rt△AED∽Rt△ADB,Rt△AFD∽Rt△ADC,根据相似三角形的性质得以证明.
解答:证明:如图,连接DE,
∵AD是圆O的直径,
∴∠AED=90°.
又∵BC切圆O于点D,
∴AD⊥BC,∠ADB=90°.
在Rt△AED和Rt△ADB中,∠EAD=∠DAB,
∴Rt△AED∽Rt△ADB.
∴ .
.
即AE•AB=AD2
同理连接DF,可证Rt△AFD∽Rt△ADC,AF•AC=AD2.
∴AE•AB=AF•AC.
点评:乘积的形式通常可以转化成比例的形式,本题着重考查了两个比例相互间的转换.
解答:证明:如图,连接DE,

∵AD是圆O的直径,
∴∠AED=90°.
又∵BC切圆O于点D,
∴AD⊥BC,∠ADB=90°.
在Rt△AED和Rt△ADB中,∠EAD=∠DAB,
∴Rt△AED∽Rt△ADB.
∴
 .
.即AE•AB=AD2
同理连接DF,可证Rt△AFD∽Rt△ADC,AF•AC=AD2.
∴AE•AB=AF•AC.
点评:乘积的形式通常可以转化成比例的形式,本题着重考查了两个比例相互间的转换.

练习册系列答案
相关题目
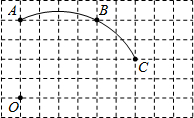 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.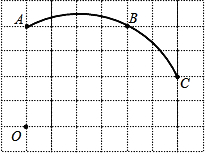 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.