题目内容
【题目】如图所示，直线AB、CD、EF相交于点O，∠AOE＝40°，∠BOC＝2∠AOC，求∠DOF.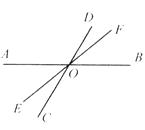 
【答案】解：设∠AOC＝x°，则∠BOC＝(2x)°. 因为∠AOC与∠BOC是邻补角，所以∠AOC+∠BOC＝180°
所以x+2x＝180
解得x＝60
所以∠AOC＝60°.因为∠DOF与∠EOC是对顶角，
所以∠DOF＝∠EOC＝∠AOC－∠AOE＝60°－40°＝20°
【解析】图形中∠BOC与∠AOC互为邻补角，结合已知条件：∠BOC＝2∠AOC，则可求出∠AOC，要求∠DOF只需求它的对顶角∠EOC即可，本题可用方程求解．
【考点精析】本题主要考查了对顶角和邻补角的相关知识点，需要掌握两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个才能正确解答此题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某商场为了吸引顾客，举行抽奖活动，并规定：顾客每购买100元的商品，就可随机抽取一张奖券，抽得奖券“紫气东来”、“花开富贵”、“吉星高照”，就可以分别获得100元、50元、20元的购物券，抽得“谢谢惠顾”不赠购物券；如果顾客不愿意抽奖，可以直接获得购物券10元。小明购买了100元的商品，他看到商场公布的前10000张奖券的抽奖结果如下：
奖券种类 | 紫气东来 | 花开富贵 | 吉星高照 | 谢谢惠顾 |
出现张数（张） | 500 | 1000 | 2000 | 6500 |
（1）求“紫气东来”奖券出现的频率；
（2）请你帮助小明判断，抽奖和直接获得购物卷，哪种方式更合算？并说明理由。