题目内容
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
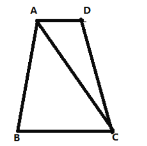
(1)求线段![]() 的长;
的长;
(2)联结![]() ,交对角线
,交对角线![]() 于点
于点![]() ,求
,求![]() 的余切值.
的余切值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)作BE垂直AC于E,由BC求出BE的长,再根据BE的长求出AE的长,即可求出AC的长.
(2)由题意做OP垂直BC于P,根据三角形相似,求出OC的长,再根据![]() 求出OP,PC即可求出∠OBC的余切,即
求出OP,PC即可求出∠OBC的余切,即![]() 的余切值.
的余切值.
(1)
作BE垂直AC于E,
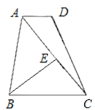
∵![]() ,BC=5,
,BC=5,
∴EC=3,
由勾股定理可得:BE=4,
∵∠BAC=45°,
∴AE=BE,
∴AE=4,
∴AC=AE+EC=4+3=7,
即AC的长为7,
由BC求出BE的长,再根据BE的长求出AE的长,即可求出AC的长.
(2)
由题意作图,
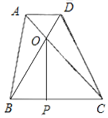
∵AD‖BC,
∴∠OBC=∠ADO,
∴AO:OC=AD:BC(平行线分线段成比例),
∴AO:OC=2:5,
∵AC=7,
∴OC=5,
做OP垂直BC于P,
∵![]() ,
,
∴PC=3,
由勾股定理可得:OP=4,
∵BC=5,
∴BP=2,
∴![]() 的余切值为
的余切值为![]() =
=![]() =
=![]() ,
,
即![]() 的余切值为
的余切值为![]() .
.

练习册系列答案
相关题目