题目内容
在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称,
与点B关于AE对称, 与AE交于点F,连接
与AE交于点F,连接 ,
, ,FC。下列结论:①
,FC。下列结论:① ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ 。其中正确的是( )
。其中正确的是( )
| A.①② | B.①②④ | C.③④ | D.①②③④ |
B
解析试题分析:①因为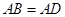 ,而F为BB’中点,经过证明,可得
,而F为BB’中点,经过证明,可得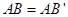 ,所以
,所以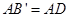 ②因为F、E分别为BB’和BC中点,所以FE∥B’C,因为
②因为F、E分别为BB’和BC中点,所以FE∥B’C,因为 为直角,所以
为直角,所以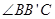 为直角,因为
为直角,因为 ,
,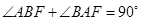 ,所以
,所以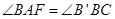 ,而
,而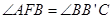 ,
,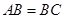 ,所以△ABF≌△BCB’,所以
,所以△ABF≌△BCB’,所以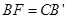 ,又
,又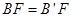 ,所以
,所以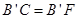 ,所以△FCB’为等腰直角三角形④因为FE∥B’C,所以
,所以△FCB’为等腰直角三角形④因为FE∥B’C,所以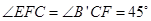 ,而
,而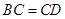 ,
,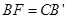 ,又
,又 ,
,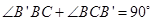 ,所以
,所以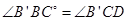 ,所以△BFC≌△CB’D,所以
,所以△BFC≌△CB’D,所以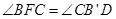 ,而
,而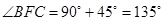 ,所以
,所以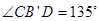
考点:全等三角形的判断,中位线的应用,平行线的性质
点评:题目难度一般,学生做此题时应该谨慎,利用全等三角形的性质,得出对应边相等,对应角相等

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=
已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF= 18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
 如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.
如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.