题目内容
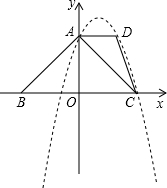 在梯形ABCD中,AD∥BC,BA⊥AC,∠B=45°,AD=2,BC=6,以BC所在直线为x轴,建立如图所示的平面直角坐标系,点A在y轴上.
在梯形ABCD中,AD∥BC,BA⊥AC,∠B=45°,AD=2,BC=6,以BC所在直线为x轴,建立如图所示的平面直角坐标系,点A在y轴上.
(1)求过A、D、C三点的抛物线的解析式.
(2)求△ADC的外接圆的圆心M的坐标,并求⊙M的半径.
(3)E为抛物线对称轴上一点,F为y轴上一点,求当ED+EC+FD+FC最小时,EF的长.
(4)设Q为射线CB上任意一点,点P为对称轴左侧抛物线上任意一点,问是否存在这样的点P、Q,使得以P、Q、C为顶点的△与△ADC相似?若存在,直接写出点P、Q的坐标;若不存在,则说明理由.
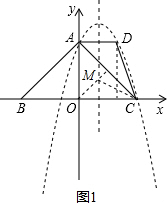 解:(1)由题意知C(3,0)、A(0,3).
解:(1)由题意知C(3,0)、A(0,3).如图1,过D作x轴垂线,由矩形性质得D(2,3).
由抛物线的对称性可知抛物线与x轴另一交点为(-1,0).
设抛物线的解析式为y=a(x+1)(x-3).
将(0,3)代入得a=-1,所以y=-x2+2x+3.
(2)由外接圆知识知M为对称轴与AC中垂线的交点.
由等腰直角三角形性质得OM平分∠AOC,即yOM=x,
∴M(1,1).
连MC得MC=
 ,即半径为
,即半径为 .
.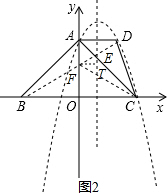
(3)如图2,由对称性可知:当ED+EC+FD+FC最小时,E为对称轴与AC交点,F为BD与y轴交点,
∵∠B=45°,∠AOB=90°,
∴AO=BO=3,故B点坐标为:(-3,0),
再利用D(2,3),代入y=ax+b,得:
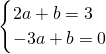 ,
,解得:
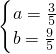 ,
,故BD直线解析式为:y=
 x+
x+ ,
,当x=0,y=
 ,根据对称轴为直线x=1,则y=2,
,根据对称轴为直线x=1,则y=2,故F(0,
 )、E(1,2),
)、E(1,2),EF=
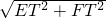 =
=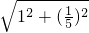 =
=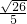 .
.
(4)可得△ADC中,AD=2,AC=
 ,DC=
,DC= .
.假设存在,显然∠QCP<90°,则∠QCP=45°或∠QCP=∠CAD.
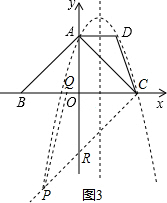
如图3,当∠QCP=45°时,OR=OC=3,
则R点坐标为(0,-3),将C,R代入y=ax+b得出:
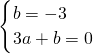 ,
,解得:
 ,
,这时直线CP的解析式为y=x-3,同理可得另一解析式为:y=-x+3.
当直线CP的解析式为y=x-3时,
则x-3=-x2+2x+3,
解得:x1=-2,x2=3,
可求得P(-2,-5),
故PC=
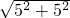 =5
=5 .
.设CQ=x,则
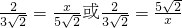 ,
,解得:x=
 或x=15.
或x=15.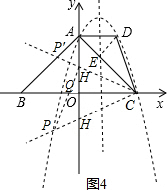
∴Q (-
 ,0)或(-12,0).
,0)或(-12,0).当y=-x+3即P与A重合时,CQ=y,则
 =
=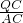 ,
,即
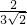 =
=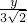 ,或
,或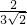 =
=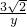 ,
,解得CQ=2或9,
故Q (1,0)或(-6,0).
如图4,当∠QCP=∠ACD时,设CP交y轴于H,连接ED,则ED⊥AC,
∴DE=
 ,EC=2
,EC=2 ,
,易证:△CDE∽△CHQ,
所以
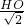 =
=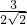 ,
,∴HO=
 .
.可求HC的解析式为y=
 x-
x- .
.联解
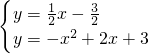 ,
,得P(-
 ,-
,- ),PC=
),PC=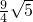 .
.设CQ=x,知
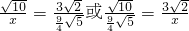 ,
,∴x=
 或x=
或x= ,
,∴Q(-
 ,0)或(-
,0)或(- ,0).
,0).同理当H在y轴正半轴上时,HC的解析式为y=-
 x+
x+ .
.∴P’(-
 ,
, ),
),∴PC=
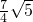 .
.∴
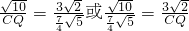 ,
,∴CQ=
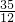 或
或 ,所以Q(
,所以Q( ,0)或(-
,0)或(- ,0).
,0).综上所述,P1(-2,-5)、Q1(-
 ,0)或(-12,0);P2(0,3)、Q2(1,0)或(-6,0);P3(-
,0)或(-12,0);P2(0,3)、Q2(1,0)或(-6,0);P3(- ,-
,- )、Q3(-
)、Q3(- ,0)或(-
,0)或(- ,0);P4(-
,0);P4(- ,
, )、Q4(
)、Q4( ,0)或(-
,0)或(- ,0).
,0).分析:(1)过D作x轴垂线,由抛物线的对称性可知抛物线与x轴另一交点为(-1,0).再根据交点式即可求出过A、D、C三点的抛物线的解析式;
(2)由外接圆知识知M为对称轴与AC中垂线的交点.由等腰直角三角形性质可得M点的坐标,连MC得MC=
 ,即为半径;
,即为半径;(3)由对称性可知:当ED+EC+FD+FC最小时,E为对称轴与AC交点,F为BD与y轴交点,再根据待定系数法求出BD直线解析式,从而得到E,F的坐标,再根据两点坐标公式即可求得EF的长;
(4)先求出直线CP的解析式为y=x-3或y=-x+3,再分情况讨论求得以P、Q、C为顶点的三角形与△ADC相似时点P、Q的坐标.
点评:此题主要考查了二次函数的综合题型,其中涉及到的知识点有抛物线的对称轴公式和三角函数关系等知识,利用三角形三边关系得出|TM-TF|是解题关键.

练习册系列答案
相关题目
 10、如图,在梯形ABCD中,若AB∥CD,BD=AD,∠BCD=110°,∠CBD=30°,则∠ADC=
10、如图,在梯形ABCD中,若AB∥CD,BD=AD,∠BCD=110°,∠CBD=30°,则∠ADC= 如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.
如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之. 如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E. 如图,在梯形ABCD中,AD∥BC,AB=AD,BD=BC,∠A=100°,则∠BDC的度数为( )
如图,在梯形ABCD中,AD∥BC,AB=AD,BD=BC,∠A=100°,则∠BDC的度数为( )