题目内容
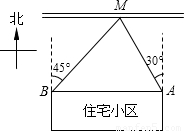
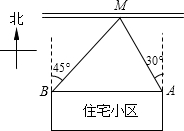 如图,是一个实际问题抽象的几何模型,已知A、B之间的距离为300m,求点M到直线AB的距离.(精确到整数)(参考数据:
如图,是一个实际问题抽象的几何模型,已知A、B之间的距离为300m,求点M到直线AB的距离.(精确到整数)(参考数据:| 3 |
| 2 |
分析:过点M作AB的垂线MN,垂足为N,那么MN就是所求的距离,在直角三角形MNB和直角三角形AMN中,MN为共有的边,可用MN表示出BN和AN,然后根据AB的长为300,来求出MN的长.
解答:解:过点M作AB的垂线MN,垂足为N.
∵M位于B的北偏东45°方向上
∴∠MBN=45°,BN=MN
∵M位于A的北偏西30°方向上
∴∠MAN=60°,AN=
=
∵AB=300
∴AN+NB=300,
∴MN+
=300
∴MN≈190.

∵M位于B的北偏东45°方向上
∴∠MBN=45°,BN=MN
∵M位于A的北偏西30°方向上
∴∠MAN=60°,AN=
| MN |
| tan60° |
| MN | ||
|
∵AB=300
∴AN+NB=300,
∴MN+
| MN | ||
|
∴MN≈190.
点评:两个直角三角形有公共的直角边时,利用这条公共边是解决此类题目的基本出发点.

练习册系列答案
相关题目
 ≈1.7,
≈1.7,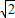 ≈1.4)
≈1.4)
 ≈1.7,
≈1.7, ≈1.4)
≈1.4)
 ≈1.7,
≈1.7, ≈1.4)
≈1.4)
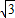 ≈1.7,
≈1.7,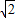 ≈1.4)
≈1.4)