题目内容
 如图所示,在四边形ABCD中,已知:AB∥CD,AD=BC,∠A=∠B=90°,E是AB上一点,且DE=DC,过点C作CF⊥DE,垂足为点F.
如图所示,在四边形ABCD中,已知:AB∥CD,AD=BC,∠A=∠B=90°,E是AB上一点,且DE=DC,过点C作CF⊥DE,垂足为点F.
(1)证明:DA=CF;
(2)猜想:EB与EF的大小关系,请证明你的猜想.
(1)证明:∵AB∥CD,
∴∠CDF=∠AEF.
在△AED和△FDC中
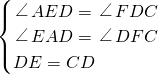 ,
,
∴△AED≌△FDC(AAS).
∴DA=CF.
(2)猜想:EB=EF,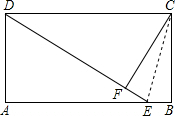
证明如下:连接CE;
∵DA=CF,AD=BC,
∴CB=CF.
在Rt△CBE和Rt△CFE中
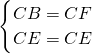 ,
,
∴Rt△CBE≌Rt△CFE(HL),
∴BE=EF.
分析:本题条件比较充分,第一问的证明是不难的.要证DA=CF,只需△AED≌△FDC,要证△AED≌△FDC,现有条件DE=DC需∠CDF=∠AEF,∠EAD=∠DFC而由平行和垂直都可证得.
点评:本题考查了三角形全等的判定及性质;有的问题在证明时要作辅助线.作法要根据需要而定.
∴∠CDF=∠AEF.
在△AED和△FDC中
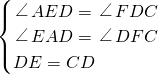 ,
,∴△AED≌△FDC(AAS).
∴DA=CF.
(2)猜想:EB=EF,

证明如下:连接CE;
∵DA=CF,AD=BC,
∴CB=CF.
在Rt△CBE和Rt△CFE中
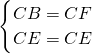 ,
,∴Rt△CBE≌Rt△CFE(HL),
∴BE=EF.
分析:本题条件比较充分,第一问的证明是不难的.要证DA=CF,只需△AED≌△FDC,要证△AED≌△FDC,现有条件DE=DC需∠CDF=∠AEF,∠EAD=∠DFC而由平行和垂直都可证得.
点评:本题考查了三角形全等的判定及性质;有的问题在证明时要作辅助线.作法要根据需要而定.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 22、如图所示,在四边形ABCD中,已知:AB:BC:CD:DA=2:2:3:1,且∠B=90°,求∠DAB的度数.
22、如图所示,在四边形ABCD中,已知:AB:BC:CD:DA=2:2:3:1,且∠B=90°,求∠DAB的度数. 11、如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为
11、如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 如图所示,在四边形ABCD中,∠BAD=90°,∠B=75°,∠ADC=135°,AB=AD=
如图所示,在四边形ABCD中,∠BAD=90°,∠B=75°,∠ADC=135°,AB=AD= 9、如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
9、如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( ) 如图所示,在四边形ABCD中,∠A=90°,AB=9,BC=20,CD=25,AD=12,求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠A=90°,AB=9,BC=20,CD=25,AD=12,求四边形ABCD的面积.