题目内容
 一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是
一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是
- A.5cm
- B.6cm
- C.(
 )cm
)cm - D.(
 )cm
)cm
B
分析:根据相似三角形的周长的比等于相似比可求△DEF的周长,求出EF的长是解决本题的关键.
解答: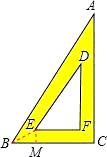 解:∵斜边AB=8cm,∠A=30°,
解:∵斜边AB=8cm,∠A=30°,
∴BC=4cm,AC=4 cm,周长是12+4
cm,周长是12+4 cm,
cm,
连接BE,过E作EM⊥BC于M,
则∠EBC=30°,EM=1cm,
∴BM= cm.
cm.
则EF=4-1- =3-
=3- cm.
cm.
∴△ABC∽△DEF,
相似比是 =
=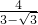 ,
,
相似三角形周长的比等于相似比,
因而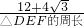 =
=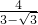 ,
,
解得△DEF的周长是6cm.
故选B.
点评:本题考查了相似三角形的性质,相似三角形的周长的比等于相似比.
分析:根据相似三角形的周长的比等于相似比可求△DEF的周长,求出EF的长是解决本题的关键.
解答:
 解:∵斜边AB=8cm,∠A=30°,
解:∵斜边AB=8cm,∠A=30°,∴BC=4cm,AC=4
 cm,周长是12+4
cm,周长是12+4 cm,
cm,连接BE,过E作EM⊥BC于M,
则∠EBC=30°,EM=1cm,
∴BM=
 cm.
cm.则EF=4-1-
 =3-
=3- cm.
cm.∴△ABC∽△DEF,
相似比是
 =
=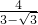 ,
,相似三角形周长的比等于相似比,
因而
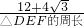 =
=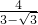 ,
,解得△DEF的周长是6cm.
故选B.
点评:本题考查了相似三角形的性质,相似三角形的周长的比等于相似比.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 19、已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线l上向右平移.当点E与点B重合时,点A恰好落在三角板的斜边DF上.
19、已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线l上向右平移.当点E与点B重合时,点A恰好落在三角板的斜边DF上. (2012•荆州)已知:直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )
(2012•荆州)已知:直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( )
 已知:直线l1∥l2,将一块含30°角的直角三角板如图所示放置,若∠1=25°,则∠2=
已知:直线l1∥l2,将一块含30°角的直角三角板如图所示放置,若∠1=25°,则∠2= 如图,有一块含30°角的直角三角板(∠A=30°,∠C=90°)的一个顶点放在直尺的一边上,若∠1=20°.那么∠2的度数是
如图,有一块含30°角的直角三角板(∠A=30°,∠C=90°)的一个顶点放在直尺的一边上,若∠1=20°.那么∠2的度数是