题目内容
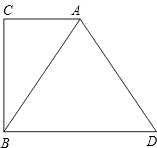
已知:如图,在Rt△ABC中,∠C=90°,∠ABC=60°,BC长为 p,BBl是∠ABC的平分线交AC于点B1,过B1作B1B2⊥AB于点B2,过B2作B2B3∥BC交AC于点B3,过B3作B3B4⊥AB于点B4,过B4作B4B5∥BC交AC于点B5,过B5作B5B6⊥AB于点B6,…,无限重复以上操作.设b=BBl,b1=B1B2,b2=B2B3,b3=B3B4,b4=B4B5,…,bn=BnBn+1,….
p,BBl是∠ABC的平分线交AC于点B1,过B1作B1B2⊥AB于点B2,过B2作B2B3∥BC交AC于点B3,过B3作B3B4⊥AB于点B4,过B4作B4B5∥BC交AC于点B5,过B5作B5B6⊥AB于点B6,…,无限重复以上操作.设b=BBl,b1=B1B2,b2=B2B3,b3=B3B4,b4=B4B5,…,bn=BnBn+1,….(1)求b,b3的长;
(2)求bn的表达式.(用含p与n的式子表示,其中n是正整数)

【答案】分析:(1)能够根据30°的直角三角形中各边的关系进行计算:三边从小到大的比是1: :2,根据这一比值进行计算;
:2,根据这一比值进行计算;
(2)不难发现:当n是正整数时,下一条边的长度总是上一条边的长度的 倍.
倍.
解答:解:(1)b=2p,
在Rt△B1B2中,b1=P,
同理:b2=
 ,b3=
,b3= .
.
(2)同(1)得:b4=( )2p,
)2p,
∴bn=( )n-1p(n是正整数).
)n-1p(n是正整数).
点评:此题要非常熟悉30°的直角三角形三边之间的关系,同时正确理解题意充分发挥已知条件的作用也很重要.
 :2,根据这一比值进行计算;
:2,根据这一比值进行计算;(2)不难发现:当n是正整数时,下一条边的长度总是上一条边的长度的
 倍.
倍.解答:解:(1)b=2p,
在Rt△B1B2中,b1=P,
同理:b2=

 ,b3=
,b3= .
.(2)同(1)得:b4=(
 )2p,
)2p,∴bn=(
 )n-1p(n是正整数).
)n-1p(n是正整数).点评:此题要非常熟悉30°的直角三角形三边之间的关系,同时正确理解题意充分发挥已知条件的作用也很重要.

练习册系列答案
相关题目
 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.