题目内容
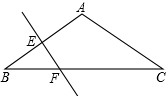 已知,在△ABC中,AB=AC,∠A=120°,EF垂直平分AB,若BC=30,则CF=________.
已知,在△ABC中,AB=AC,∠A=120°,EF垂直平分AB,若BC=30,则CF=________.
20
分析:连接AF、过A作AD⊥BC于D,再根据等腰三角形的性质求出BD= BC,由直角三角形的性质及线段垂直平分线的性质得出AF=BF,DF=
BC,由直角三角形的性质及线段垂直平分线的性质得出AF=BF,DF= AF,列出方程求出DF的长即可.
AF,列出方程求出DF的长即可.
解答: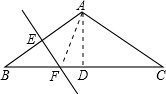 解:连接AF、过A作AD⊥BC于D,
解:连接AF、过A作AD⊥BC于D,
∵△ABC中,AB=AC,∠A=120°,BC=30,
∴∠B=∠C= =30°,BD=CD=
=30°,BD=CD= BC=
BC= ×30=15,∠BAD=60°,
×30=15,∠BAD=60°,
∵EF是线段AB的垂直平分线,
∴AF=BF,∠B=∠BAF=30°,
∴∠DAF=∠BAD-∠BAF=60°-30°=30°,
∴DF= AF,
AF,
设DF=x,则AF=BF=2x,
∴BF+DF=x+2x=15,
解得x=5.
∴DF=5,
∴CF=DF+CD=5+15=20.
故答案为:20.
点评:本题考查的是等腰三角形的性质及线段垂直平分线的性质,根据题意作出辅助线是解答此题的关键.
分析:连接AF、过A作AD⊥BC于D,再根据等腰三角形的性质求出BD=
 BC,由直角三角形的性质及线段垂直平分线的性质得出AF=BF,DF=
BC,由直角三角形的性质及线段垂直平分线的性质得出AF=BF,DF= AF,列出方程求出DF的长即可.
AF,列出方程求出DF的长即可.解答:
 解:连接AF、过A作AD⊥BC于D,
解:连接AF、过A作AD⊥BC于D,∵△ABC中,AB=AC,∠A=120°,BC=30,
∴∠B=∠C=
 =30°,BD=CD=
=30°,BD=CD= BC=
BC= ×30=15,∠BAD=60°,
×30=15,∠BAD=60°,∵EF是线段AB的垂直平分线,
∴AF=BF,∠B=∠BAF=30°,
∴∠DAF=∠BAD-∠BAF=60°-30°=30°,
∴DF=
 AF,
AF,设DF=x,则AF=BF=2x,
∴BF+DF=x+2x=15,
解得x=5.
∴DF=5,
∴CF=DF+CD=5+15=20.
故答案为:20.
点评:本题考查的是等腰三角形的性质及线段垂直平分线的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.