Question

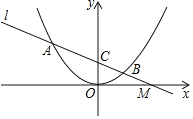
【题目】如图，已知抛物线y＝ax2过点A（﹣3，）．

（1）求抛物线的解析式；

（2）已知直线l过点A，M（，0）且与抛物线交于另一点B，与y轴交于点C，求证：MC2＝MAMB；

（3）若点P，D分别是抛物线与直线l上的动点，以OC为一边且顶点为O，C，P，D的四边形是平行四边形，求所有符合条件的P点坐标．

Answer 1

【答案】（1）y＝x2；（2）见解析；（3）P（﹣1﹣，2+）或（﹣1+，2﹣）或（﹣2，1）．

【解析】

（1）利用待定系数法即可解决问题．

（2）构建方程组确定点B的坐标，再利用平行线分线段成比例定理解决问题即可．

（3）如图2中，设P（t，t2），根据PD＝CD构建方程求出t即可解决问题．

解：（1）把点A（﹣3，）代入y＝ax2，

得到＝9a，

∴a＝，

∴抛物线的解析式为y＝x2．

（2）设直线l的解析式为y＝kx+b，则有，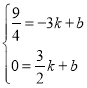

解得，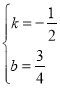

∴直线l的解析式为y＝﹣x+，

令x＝0，得到y＝，

∴C（0，），

由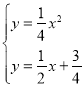，解得或，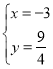

∴B（1，），

如图1中，过点A作AA1⊥x轴于A1，过B作BB1⊥x轴于B1，则BB1∥OC∥AA1，

∴＝＝＝，＝＝＝，

∴＝，

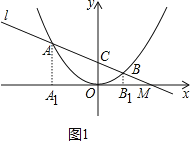
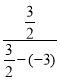即MC2＝MAMB．

（3）如图2中，设P（t，t2）

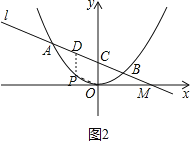
∵OC为一边且顶点为O，C，P，D的四边形是平行四边形，

∴PD∥OC，PD＝OC，

∴D（t，﹣t+），

∴|t2﹣（﹣t+）|＝，

整理得：t2+2t﹣6＝0或t2+2t＝0，

解得t＝﹣1﹣或﹣1＝或﹣2或0（舍弃），

∴P（﹣1﹣，2+）或（﹣1+，2﹣）或（﹣2，1）．